ASOCIACIÓN MADRE – HIJO
NUBE DE PUNTOS y BOX PLOT
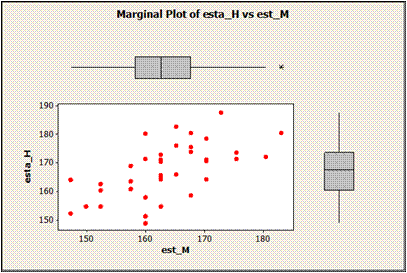
REGRESIÓN LINEAL Y ESTIMACIÓN


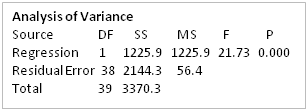
DIAGRAMA DE DISPERSIÓN
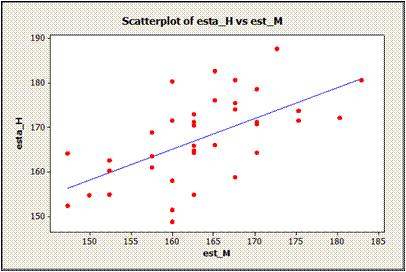
ASOCIACIÓN PADRE – HIJO
NUBE DE PUNTOS y BOX PLOT
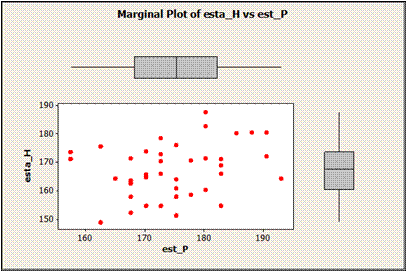
REGRESIÓN LINEAL Y ESTIMACIÓN


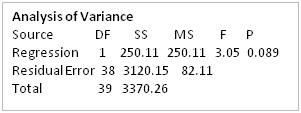
DIAGRAMA DE DISPERSIÓN
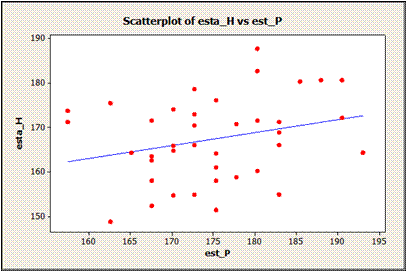
Sigue leyendo
ASOCIACIÓN MADRE – HIJO
NUBE DE PUNTOS y BOX PLOT

REGRESIÓN LINEAL Y ESTIMACIÓN



DIAGRAMA DE DISPERSIÓN

ASOCIACIÓN PADRE – HIJO
NUBE DE PUNTOS y BOX PLOT

REGRESIÓN LINEAL Y ESTIMACIÓN



DIAGRAMA DE DISPERSIÓN

Sigue leyendo
ASOCIACIÓN MADRE – HIJO
NUBE DE PUNTOS: Aproximación intuitiva
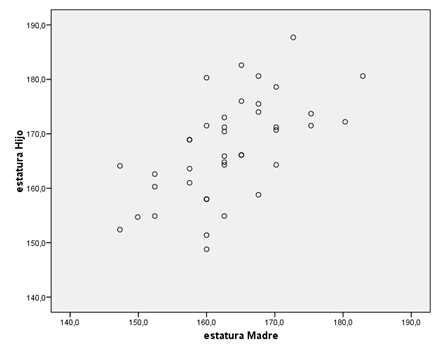
REGRESIÓN LINEAL Y ESTIMACIÓN
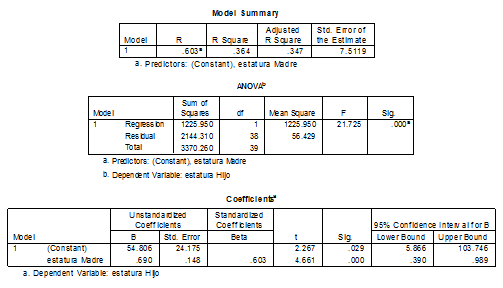
DIAGRAMA DE DISPERSIÓN

ASOCIACIÓN PADRE – HIJO
NUBE DE PUNTOS: Aproximación intuitiva
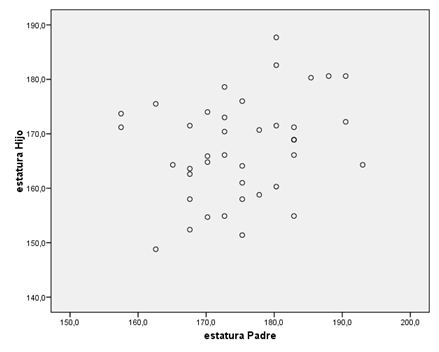
REGRESIÓN LINEAL Y ESTIMACIÓN
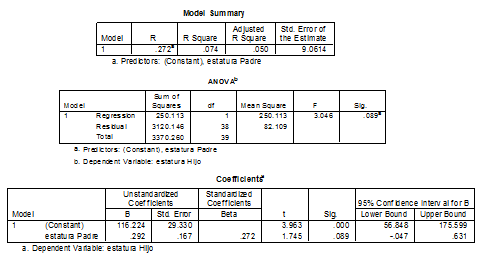
DIAGRAMA DE DISPERSIÓN
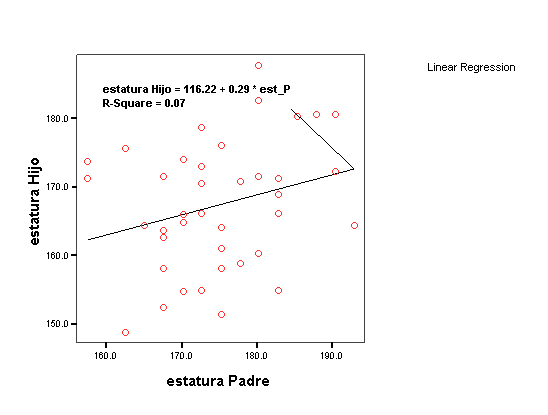
Sigue leyendo
ASOCIACIÓN MADRE – HIJO
NUBE DE PUNTOS: Aproximación intuitiva
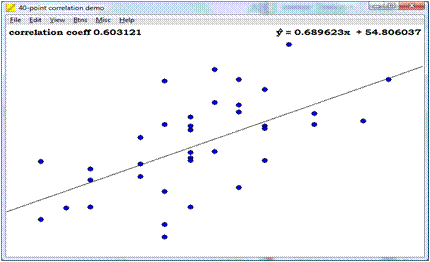
REGRESIÓN LINEAL Y ESTIMACIÓN
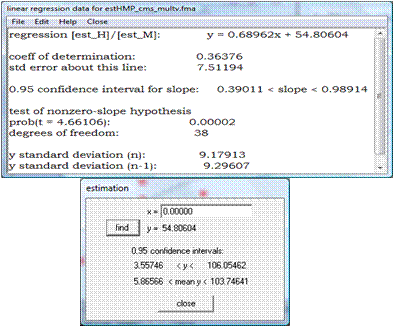
DIAGRAMA DE DISPERSIÓN
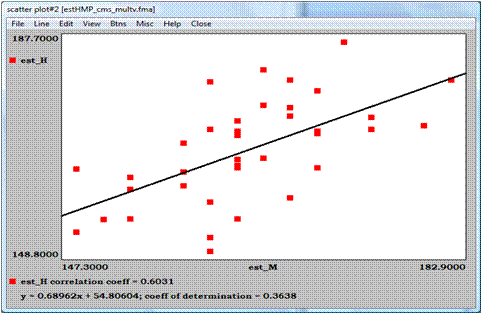
ASOCIACIÓN PADRE – HIJO
NUBE DE PUNTOS: Aproximación intuitiva
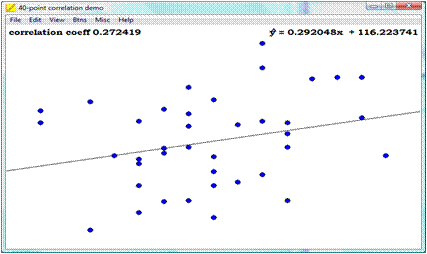
REGRESIÓN LINEAL Y ESTIMACIÓN
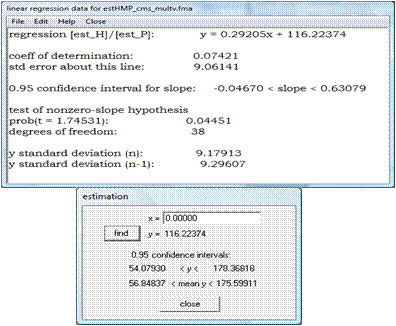
DIAGRAMA DE DISPERSIÓN
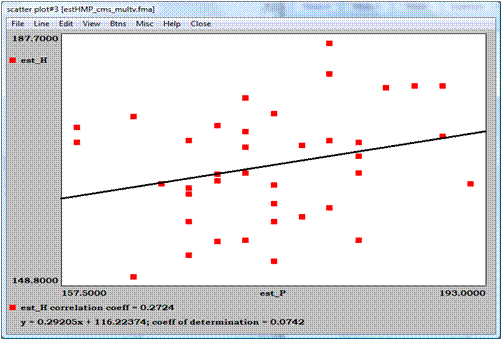
Sigue leyendo
BOX PLOT
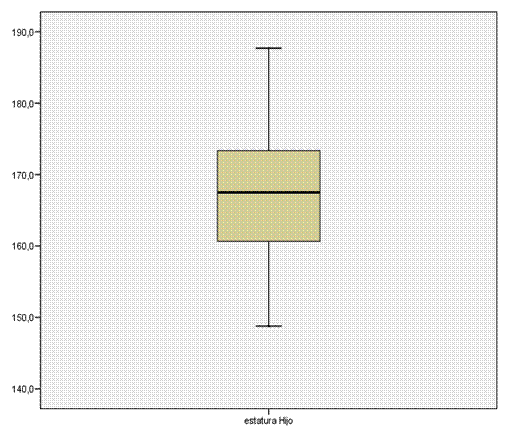
RESUMEN DESCRIPTIVO
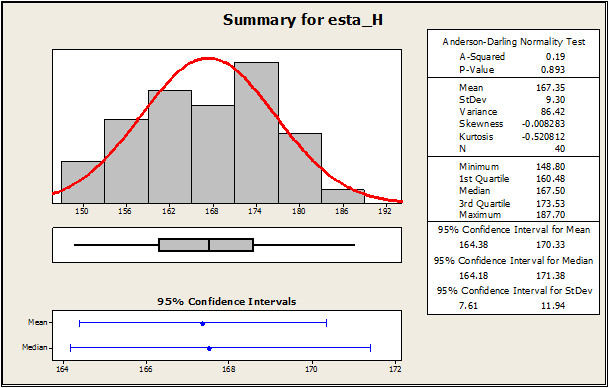
A MANERA DE COROLARIO…
ANÁLISIS EXPLORATORIO
ESTADÍSTICOS DESCRIPTIVOS

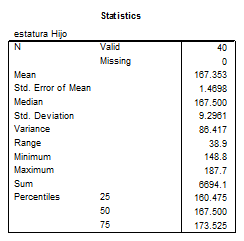
HISTOGRAMA Y NORMAL
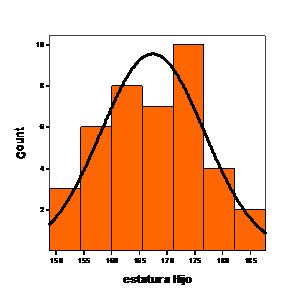
BOX PLOT (vertical)

Sigue leyendo

b) Análisis Exploratorio
OVERALL
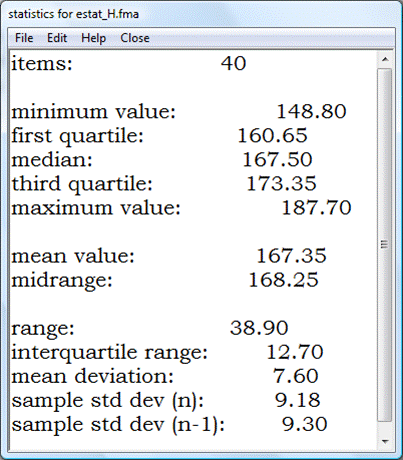
BOXPLOT
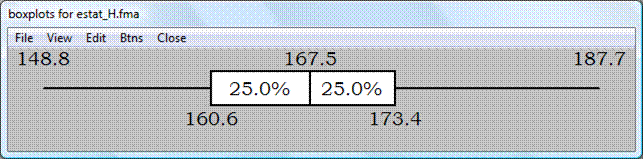
TABLA DE FRECUENCIAS
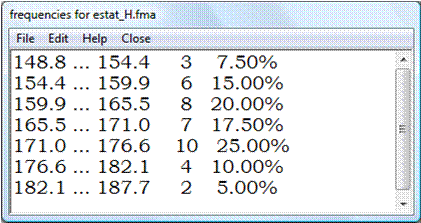
HISTOGRAMA y POLÍGONO
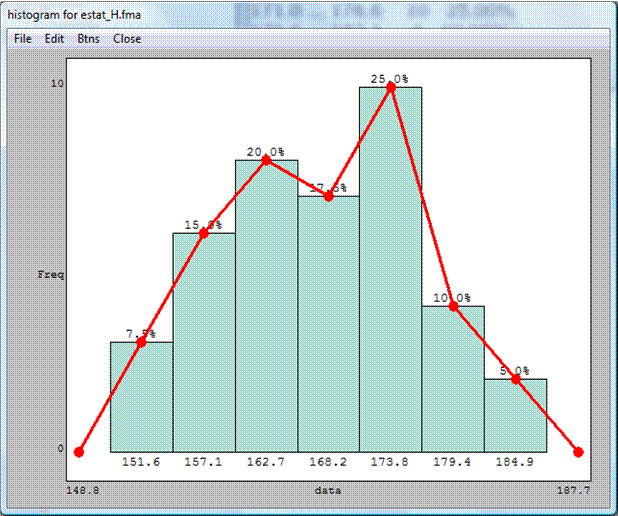
HISTOGRAMA y NORMAL
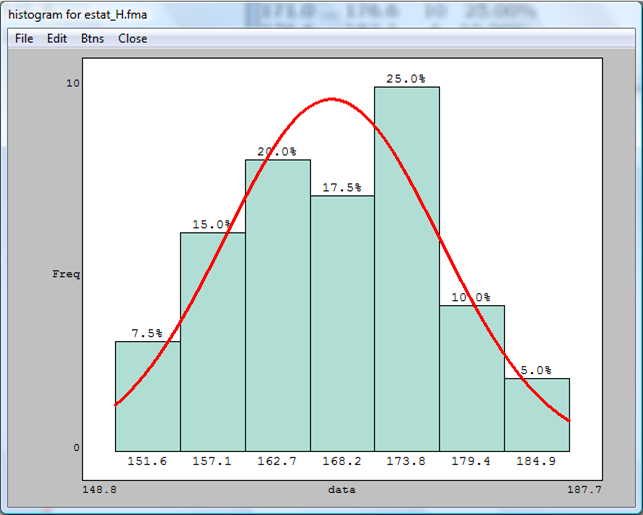
Sigue leyendo
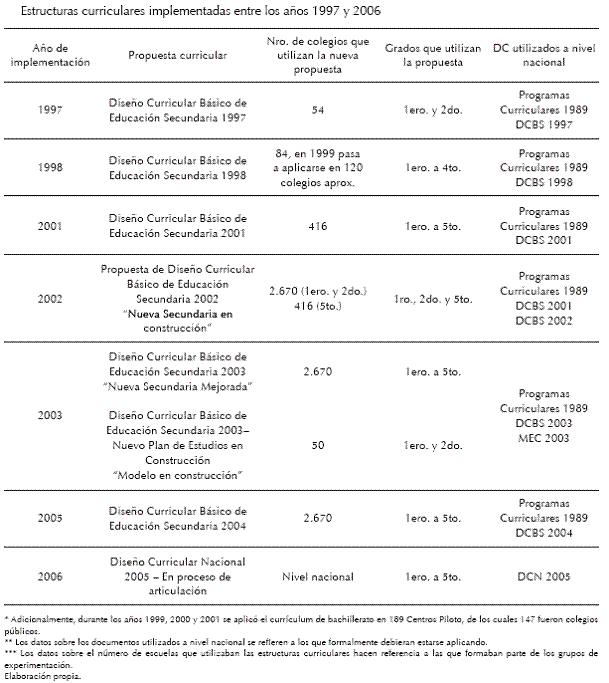
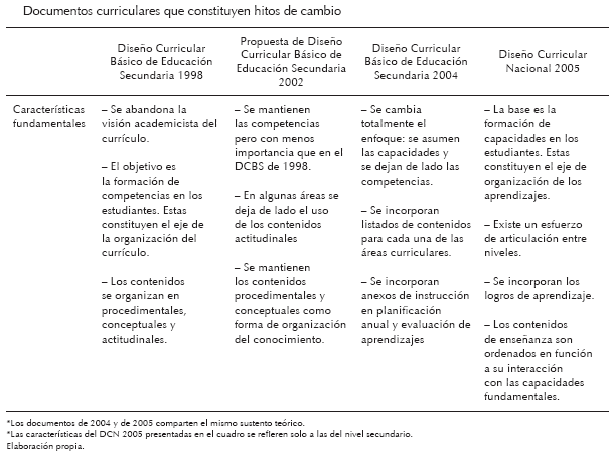
Ejemplo 02: Área de la superficie del sólido de revolución
Se desea calcular el área de la superficie obtenida al rotar un arco completo de la cicloide

, alrededor de la tangente a la cicloide en su punto más alto.
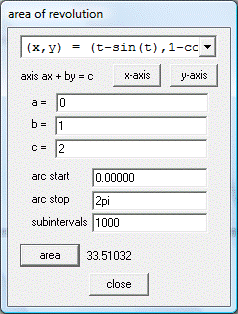
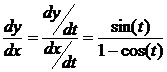
la pendiente de la tangente es
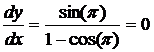
, entonces y = 2 es la ecuación de la tangente.

La distancia del punto (x;y) de la cicloide a la recta tangente es 2 – y, por lo tanto el área pedida es:
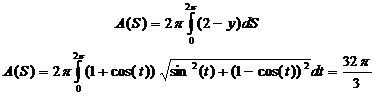 Sigue leyendo
Sigue leyendo
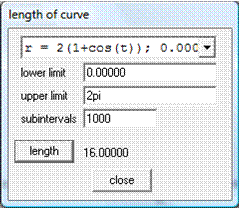
Longitud del arco de una curva
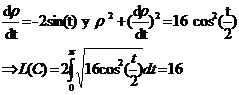
Sólidos de Revolución
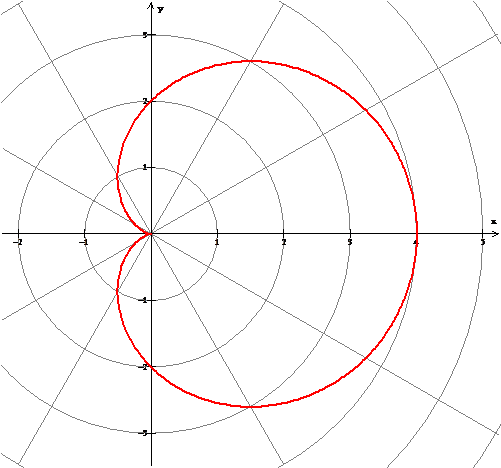
A continuación se presentan dos ejemplos a partir de la figura acotada por un arco completo de la cicloide
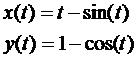
y el eje X.
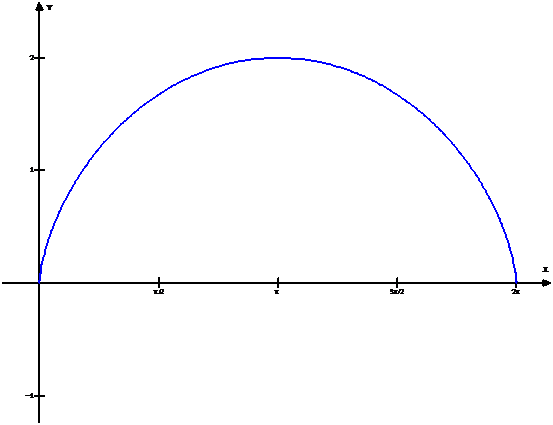
Ejemplo 01: Volumen del sólido de revolución
Si nos piden calcular el volumen del sólido formado por rotación de la figura acotada por un arco completo de la cicloide

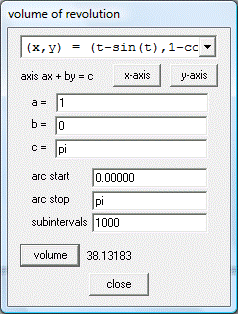
De donde:
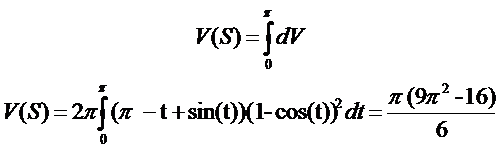

1. Preliminares
Cabe precisar que la introducción de las Tecnologías de la Información y de la Comunicación en el área de matemática de la educación básica y superior generan en el docente una serie de interrogantes: ¿De qué manera, en qué momento y cómo se van a introducir las nuevas tecnologías en las sesiones de clase? ¿Existe material bibliográfico referente a la incorporación de las nuevas tecnologías? ¿Se cuenta con la infraestructura idónea? En esta línea, hace once años, De Moura Castro en “La Educación en la Era de la Informática” (New York: B.I.D., 1998, p.121) propuso que:
“La educación debe cambiar a fin de preparar debidamente a los ciudadanos del futuro para funcionar en una sociedad en cambio continuo. Por consiguiente, es necesario reemplazar el paradigma actual de la educación (la producción masiva de ciudadanos con conocimientos prefabricados y títulos que los habilitan para una larga carrera) con modelos pedagógicos que doten a los ciudadanos de aptitudes para aprender durante toda la vida en una sociedad en la cual las tecnologías de la comunicación y la información son uno de los pilares de la infraestructura”.
2. Tópicos de cálculo integral
A continuación, a manera de ejemplo, se presenta la aplicación del Winplot en tópicos de cálculo integral en el plano:
Área de una región en el plano
Ejemplo: Si queremos encontrar el área de la región acotada por las curvas f(x) = x^3- 6x^2+ 8x y g(x) = x^2 – 4x.
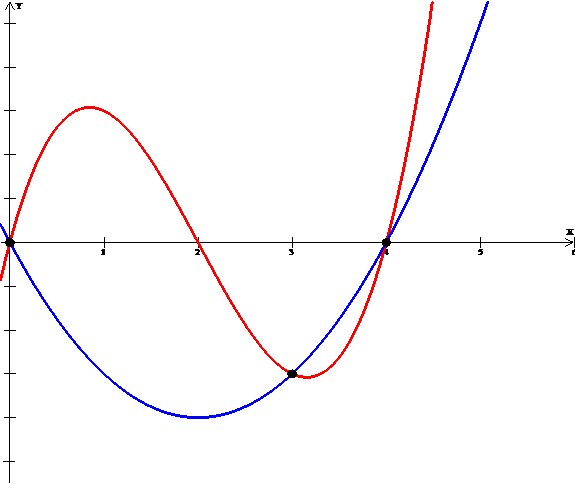
El valor de dicha área es dado por la integral definida de la función |f(x) – g(x)|, con límite inferior igual a 0 y límite superior igual a 4, es decir:
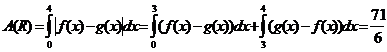
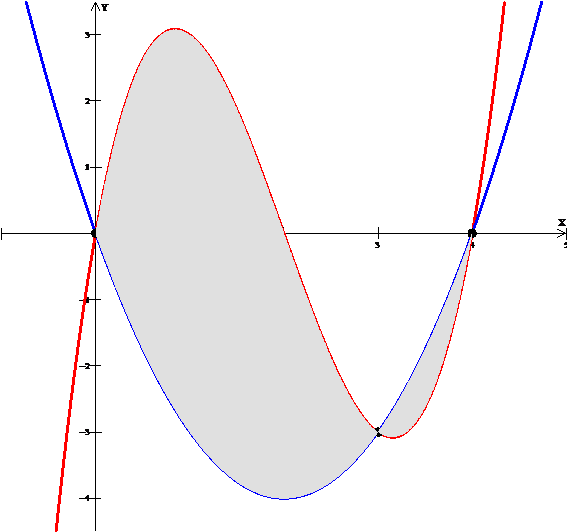
Por lo tanto: A(R) =11,25001 + 0,58333 =11,83334 (aprox.) Sigue leyendo