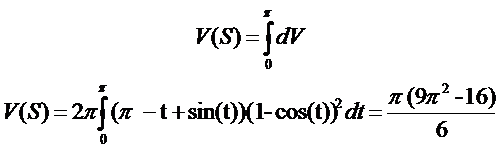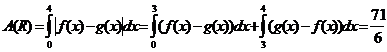Archivo por meses: mayo 2009

APLICACIÓN DEL WINPLOT EN TÓPICOS DE CÁLCULO INTEGRAL EN EL PLANO (parte III)

Deja una respuesta
[Visto: 3287 veces]

Ejemplo 02: Área de la superficie del sólido de revolución

Se desea calcular el área de la superficie obtenida al rotar un arco completo de la cicloide

, alrededor de la tangente a la cicloide en su punto más alto.

Primero, seleccionamos la ventana One, luego la opción Measurement, a continuación la opción Surface area of revolution … y aparece el recuadro area of revolution. En este recuadro, debajo de axis ax + by = c, digitamos los valores a = 0, b = 1, c = 2, arc start = 0, arc stop = 2pi. Finalmente, para hallar el área de la superficie, hacemos clic sobre area y nos da el valor aproximado: 33,51032 (ver recuadro adjunto)

box03

Si se opta por el cálculo infinitesimal, observamos que cuando t varía desde 0 hasta 2pi, se obtiene un arco completo de la cicloide. El punto más alto de la cicloide en este intervalo ocurre cuando t = pi; dado que

ecuac06
la pendiente de la tangente es
ecuac07

, entonces y = 2 es la ecuación de la tangente.
esferic_area
La distancia del punto (x;y) de la cicloide a la recta tangente es 2 – y, por lo tanto el área pedida es:
ecuac07 Sigue leyendo →

APLICACIÓN DEL WINPLOT EN TÓPICOS DE CÁLCULO INTEGRAL EN EL PLANO (parte II)

Deja una respuesta
[Visto: 6458 veces]

Longitud del arco de una curva

Ejemplo: Dada la cardiode p(t) = 2 (1 + cos(t)), si nos piden hallar la longitud del arco de dicha curva, ¿qué tenemos que hacer con el Winplot?

Primero, seleccionamos la ventana One, a continuación la opción Measurement, luego Arc Length… y aparece el recuadro length of curve. En este recuadro, digitamos 0 en lower limit y 2pi en upper limit. Finalmente, para obtener el valor de la longitud del arco de dicha curva, hacemos clic sobre length y nos da el resultado: 16 (ver recuadro adjunto)

box01

Si se desea verificar la respuesta, observamos que la gráfica de la cardiode es simétrica respecto del eje X; cuando t varía desde t = 0 hasta t = pi, el radio vector recorre el arco superior de la curva. Dado que p(t) = 2 (1 + cos(t)), entonces:

ecuac01

Sólidos de Revolución
A continuación se presentan dos ejemplos a partir de la figura acotada por un arco completo de la cicloide

ecuac02
y el eje X.

semicir
Ejemplo 01: Volumen del sólido de revolución

Si nos piden calcular el volumen del sólido formado por rotación de la figura acotada por un arco completo de la cicloide

ecuac03

y el eje X, alrededor del eje de simetría de la figura, lo que tenemos que hacer es seleccionar la ventana One, luego la opción Measurement, a continuación Volume of revolution … y aparece el recuadro volume of revolution. En este recuadro, debajo de axis ax + by = c, digitamos los valores a = 1, b = 0, c = pi, arc start = 0, arc stop = pi. Finalmente, para hallar el volumen del sólido de revolución, hacemos clic sobre volume y nos da el valor aproximado: 38,13183

box02

Si se opta por el cálculo infinitesimal, notamos que el eje de simetría de la figura es la recta x = pi, por lo que el volumen del tubo cilíndrico obtenido por rotación (alrededor de esta recta) del rectángulo de la figura es dV = 2pi(pi – x)y dx:

De donde:
ecuac04
surface

Sigue leyendo →

APLICACIÓN DEL WINPLOT EN TÓPICOS DE CÁLCULO INTEGRAL EN EL PLANO (parte I)

Deja una respuesta
[Visto: 6201 veces]

1. Preliminares

La enseñanza de la matemática, en un grueso de instituciones educativas de educación básica y superior, sigue siendo una enseñanza tradicional de carácter expositivo, de allí que se hace necesario e indispensable que los docentes de matemática incorporen los softwares – en particular los software libres o gratuitos – como herramientas o recursos pedagógicos que favorecen un aprendizaje por descubrimiento y el trabajo en equipo, en las sesiones de clase, en el marco de una metodología activa. Hay que destacar la utilidad del software como herramienta de verificación de resultados y como fuente de experimentación que permita al estudiante elaborar sus conjeturas, contrastarlas y avanzar en la resolución de una situación problemática.

Cabe precisar que la introducción de las Tecnologías de la Información y de la Comunicación en el área de matemática de la educación básica y superior generan en el docente una serie de interrogantes: ¿De qué manera, en qué momento y cómo se van a introducir las nuevas tecnologías en las sesiones de clase? ¿Existe material bibliográfico referente a la incorporación de las nuevas tecnologías? ¿Se cuenta con la infraestructura idónea? En esta línea, hace once años, De Moura Castro en “La Educación en la Era de la Informática” (New York: B.I.D., 1998, p.121) propuso que:

“La educación debe cambiar a fin de preparar debidamente a los ciudadanos del futuro para funcionar en una sociedad en cambio continuo. Por consiguiente, es necesario reemplazar el paradigma actual de la educación (la producción masiva de ciudadanos con conocimientos prefabricados y títulos que los habilitan para una larga carrera) con modelos pedagógicos que doten a los ciudadanos de aptitudes para aprender durante toda la vida en una sociedad en la cual las tecnologías de la comunicación y la información son uno de los pilares de la infraestructura”.

2. Tópicos de cálculo integral

A continuación, a manera de ejemplo, se presenta la aplicación del Winplot en tópicos de cálculo integral en el plano:

Área de una región en el plano

Ejemplo: Si queremos encontrar el área de la región acotada por las curvas f(x) = x^3- 6x^2+ 8x y g(x) = x^2 – 4x.


El valor de dicha área es dado por la integral definida de la función |f(x) – g(x)|, con límite inferior igual a 0 y límite superior igual a 4, es decir:

integral

Con el Winplot seleccionamos la ventana Two, luego hacemos clic sobre la opción Integrate, a continuación aparece el recuadro integrate f-g. En este recuadro digitamos, primero, los límites inferior (lower limit = 0) y superior (upper limit = 3). A continuación, seleccionamos un método de integración (por ejemplo midpoint) para obtener el valor del área de la región acotada por las curvas f(x), g(x) y las rectas x = 0 y x = 3. Si, además, se desea pintar la región en mención seleccionamos overlay y hacemos clic sobre definite.

region

Obsérvese que en la pantalla del monitor aparece cubierta o pintada la región pedida y en el recuadro integrate f-g aparece el valor aproximado del área: 11,25001.
Tener en cuenta que para calcular el área de la región acotada por las curvas g(x), f(x) y las rectas x = 3 y x = 4, en el recuadro integrate f-g, primero seleccionamos la regla de correspondencia y = x^2 – 4x y luego la regla de correspondencia y = x^3- 6x^2+ 8x. A continuación, digitamos los límites inferior (lower limit = 3) y superior (upper limit = 4); seleccionamos un método de integración (por ejemplo midpoint) para obtener el valor del área de la región acotada. Si se desea pintar la región en mención seleccionamos overlay y hacemos clic sobre definite. Obsérvese que en la pantalla del monitor aparece cubierta o pintada la región pedida y en el recuadro integrate f-g aparece el valor aproximado del área: 0,58333.

Por lo tanto: A(R) =11,25001 + 0,58333 =11,83334 (aprox.) Sigue leyendo →

Elección de software como recurso educativo

Deja una respuesta
[Visto: 2406 veces]

Hoy en día no se puede negar que las TICs forman parte del quehacer educativo, convirtiéndose no sólo en una ventaja para quien la utiliza, sino también en una necesidad. Sin embargo, el docente debe seleccionar con criterio los recursos informáticos: software educativo, material audiovisual, multimedia, apletts, Internet (web sites, WebQuest, bloggs, etc.) adecuados para reforzar los aprendizajes. De igual modo, el momento y la forma de utilizar este recurso tecnológico requiere de mucha pericia, que el docente irá perfeccionando con la práctica.

Sugerir un software educativo en particular puede tener un sesgo en relación a la eficacia y eficiencia en su uso en el área de matemática; podría darse el caso que se descarte un software en particular y sin embargo ser útil para el desarrollo de capacidades específicas de una determinada área de la educación básica (por ejemplo, en el área de matemática de secundaria se puede sugerir un software educativo por cada componente del área: Número, relaciones y funciones; Geometría y medida; Estadística y probabilidad).

En relación a la eficacia y eficiencia hay que tener en cuenta, en el momento de elegir un software educativo, lo siguiente:

• Se entiende por eficacia a la cualidad del software para alcanzar los aprendizajes esperados de una determinada unidad didáctica.

• Cuando un recurso didáctico le da dinámica a los procesos pedagógicos, se puede afirmar que es un recurso eficiente. En este contexto, el software como recurso didáctico es eficiente en la medida que optimiza las energías de los actores involucrados.

En consecuencia, al seleccionar un software educativo se debe explicitar: las características técnicas del mismo; los contenidos a tratar; definir los aprendizajes esperados e indicadores; plantear las situaciones problemáticas a resolver y plantear las actividades y/o estrategias relacionadas a los aprendizajes esperados. Cabe precisar que la elección de un software educativo en particular como recurso didáctico, necesita un sustento técnico pedagógico para su uso, dado que por sí mismo no va a resolver los desafíos y las dificultades que se desprenden de los procesos de enseñanza aprendizaje.

A continuación, se presentan – de manera sucinta – las características más relevantes de ocho programas (software) educativos relacionados con la enseñanza de la matemática:

Calculadora Gráfica

Es una calculadora que además de realizar gráficos puede ser programada para realizar una serie de cálculos numéricos y estadísticos. Dado su tamaño reducido, relativo bajo costo y fácil uso resulta ser apropiada para la mayoría de los estudiantes. La Calculadora Gráfica establece, a través de la pantalla, una relación entre la representación gráfica de una función y la representación simbólica (regla de correspondencia) de la misma.

Matlab

Es un programa de cálculo numérico que cuenta con un gran número de instrucciones que nos permiten resolver problemas científicos. Matlab (Matrix Laboratory) puede compararse con una potente calculadora científica programable. Entre sus aplicaciones a la Computación y las Matemáticas se puede mencionar el desarrollo de algoritmos; el modelado y la simulación; la exploración, visualización y análisis de datos; la creación de gráficas científicas; entre otras.

Mathematica

Es un programa de aplicación numérico y simbólico, incorpora un lenguaje de programación completo, el cual permite integrar cálculos, gráficos y texto en un mismo documento electrónico llamado cuaderno. Este programa permite al usuario trabajar en diferentes niveles, permitiendo desarrollar actividades matemáticas en cada uno de ellos.
Se puede distinguir en la estructura de este programa el Front-End (parte visible del programa, donde se encuentra el menú y los cuadernos) y el Kernel (donde se realizan los cálculos). En los cuadernos se pueden realizar cálculos numéricos y simbólicos; gráficas en dos y tres dimensiones; animaciones; ediciones de texto; programar funciones específicas; etc. En este programa existen paquetes de funciones y objetos ya programados así como una gama de formatos; esta variedad de formatos permiten al usuario leer paquetes y archivos automáticamente al abrir un cuaderno.

Derive

Es un programa de cálculo simbólico, capaz de calcular límites, derivadas, integrales, resolver toda clase de problemas numéricos y simbólicos cuyos resultados pueden representarse mediante gráficas de dos y tres dimensiones. Se puede afirmar que es un asistente matemático que tiene aplicación en la aritmética, álgebra, cálculo diferencial e integral, cálculo vectorial y matricial, programación de funciones recursivas e iteractivas, etc. Existe una versión en castellano.

Cabri-geómetre

Es un programa que permite construir y explorar objetos geométricos en el plano y en el espacio; utiliza archivos de extensión fig (figuras) y extensión mac (macros). La pantalla de trabajo consta de una barra de menú de opciones, una barra de herramientas, la ventana de diseño y una ventana de ayuda.
A través de la barra de herramientas se ejecuta la construcción y animación de los objetos geométricos; contiene las opciones: puntero (realiza la selección de objetos o transformaciones a mano alzada); puntos (para construir puntos); rectas (para construir objetos de lados rectos); curvas (para construir circunferencias, arcos y cónicas); construir (para realizar construcciones de geometría euclidiana); transformar (para hacer transformaciones geométricas); macro (para generar e incorporar archivos de extensión mac); comprobar (comprueba las construcciones geométricas realizadas); medir (para realizar mediciones y cálculos); ver (para realizar comentarios y animaciones); y, dibujo (para cambiar el aspecto de los objetos y para visualizar el sistema de coordenadas)

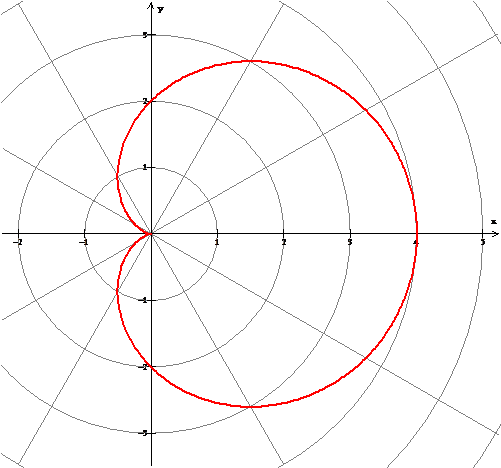
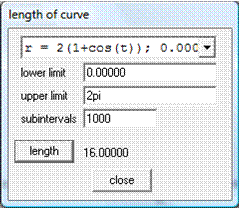
Graphmatica

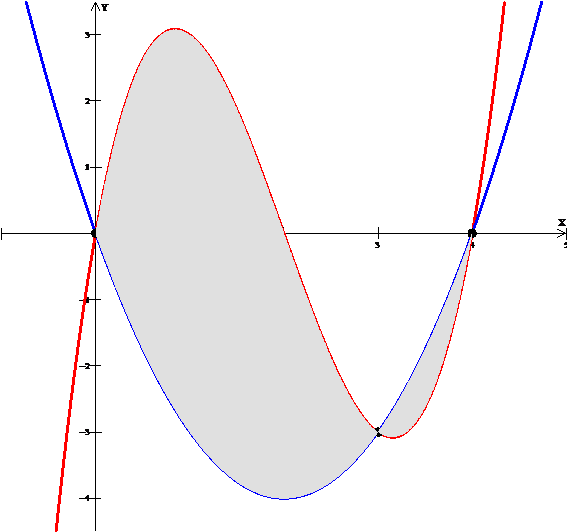
Es un programa graficador, interactivo, de ecuaciones matemáticas. Permite comparar, simultáneamente, varias gráficas; calcular el área bajo una curva; trazar la tangente a un punto; resolver inecuaciones; determinar familias de curvas. Contiene un procesador de ecuaciones y una librería completa de funciones matemáticas.
Los gráficos se pueden visualizar en coordenadas cartesianas, paramétricas, polares y campos de pendientes para ecuaciones diferenciales ordinarias (orden cuatro).Además, realiza cálculos numéricos y simbólicos: halla la derivada, la integral y puntos críticos de cualquier función en el plano cartesiano.

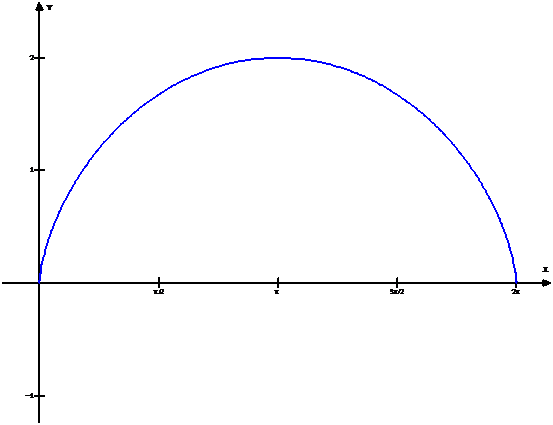
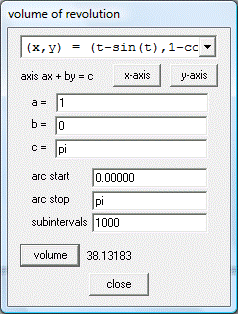
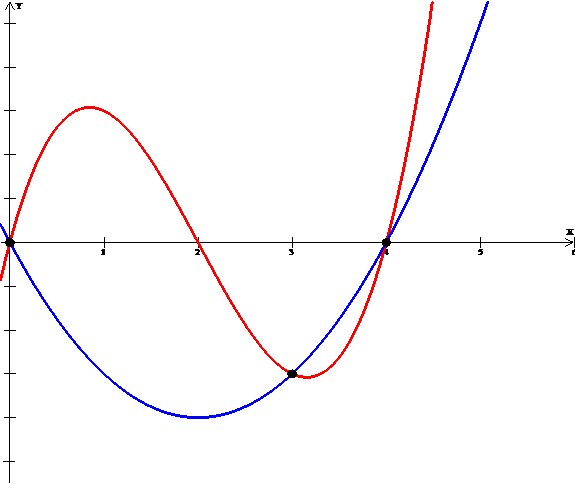
Winplot

Es un software gratuito. Es un programa graficador de dimensión 2 (ejes X, Y) y dimensión 3 (ejes X, Y, Z). Grafica curvas y superficies, las cuales se pueden visualizar en una variedad de formatos. Está compuesto de menús o ventanas, las cuales se pueden manejar sin dificultad. Cada menú tiene información detallada de las funciones que realiza.
Se pueden analizar a partir de la gráfica, sin dificultad, funciones polinomiales, racionales, exponenciales, logarítmicas, trigonométricas, paramétricas, implícitas. Calcular áreas, volúmenes. Determina gráficamente la derivada de una función así como las trayectorias de ecuaciones diferenciales.

Quiz Faber

Es un software gratuito para Windows que permite confeccionar pruebas (Quiz) multimedia, fácil y rápidamente, como documentos HTML, con la ventaja que no se necesita ningún conocimiento previo del formato HTML o Javascript. La elaboración de la prueba es hecha automáticamente por el programa.
Una vez elaborada la prueba, ésta se encuentra lista para ser publicada en Internet, en una red local (con protocolo del Intranet) o en una PC local.
Dado que tiene formato HTML se puede introducir en las pruebas objetos como imágenes, sonidos y videos, dado que es compatible con los formatos más extensos de Internet (JPEG, GIF, MEDIADOS DE, MP3, AVI, MPEG, flash de Macromedia, Apple Quick Time, Real Audio, plug-in del browser de Real Media, etc.)

Sigue leyendo →