Dicen que para muestra un botón, adjunto un video en donde se utiliza la aplicación para teléfono ( Android ) Google Goggles para dar solución a un SUDOKU!
< %flashvideo(20110113-Sudoku.flv)%>
Dicen que para muestra un botón, adjunto un video en donde se utiliza la aplicación para teléfono ( Android ) Google Goggles para dar solución a un SUDOKU!
< %flashvideo(20110113-Sudoku.flv)%>
VERSIÓN OFICIAL (MINEDU 07/12/2010):
MINEDU_07Dic10.pps
INFORME OFICIAL (OCDE):
¿QUÉ SABEN Y QUÉ PUEDEN HACER LOS ESTUDIANTES?
< %flashvideo(20101209-pisa2009.flv)%>
ESTRATEGIAS PARA LA ACCIÓN EN MÉXICO: MEJORES ESCUELAS
< %flashvideo(20101209-Mexico.flv)%>
Sigue leyendo
< %flashvideo(20101117-21Century.flv)%>
K-12 Students Today
< %flashvideo(20101118-Kids.flv)%>
…y EL PROFESOR?
Sigue leyendo
SITE 3.0
< %flashvideo(20101117-site3.flv)%>
SITE 4.0
< %flashvideo(20101117-site4.flv)%>
Sigue leyendo
< %flashvideo(20101105-TvsM.flv)%> Sigue leyendo


Curiosas “coincidencias”, no?… Sigue leyendo
PRIMER GRADO DE SECUNDARIA
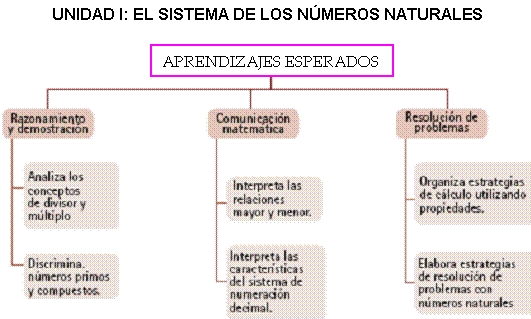
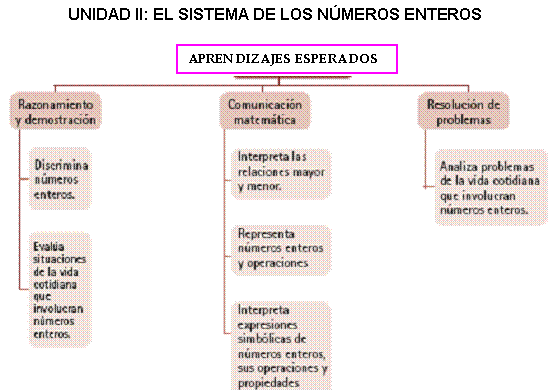
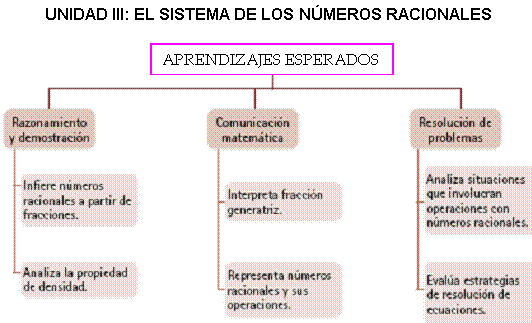
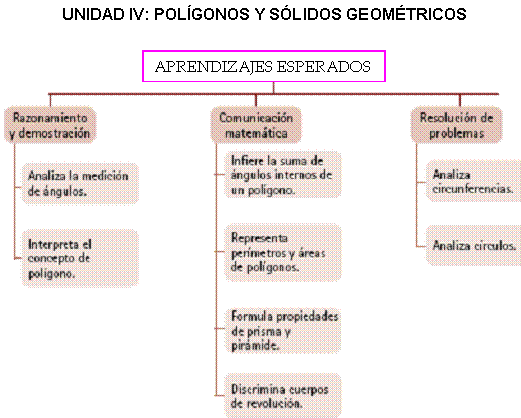
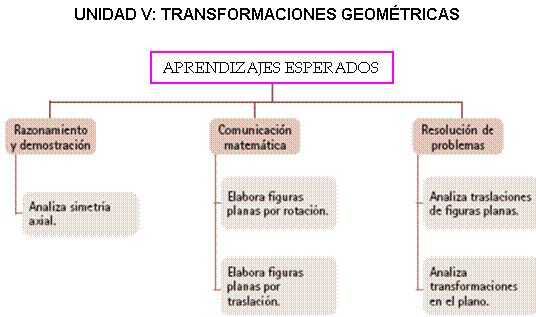
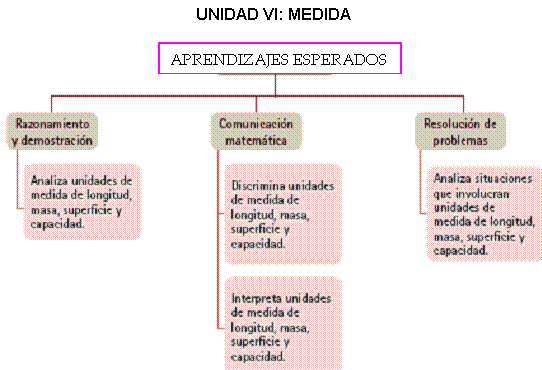

SEGUNDO GRADO DE SECUNDARIA
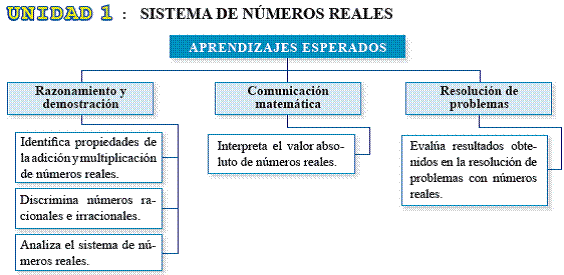
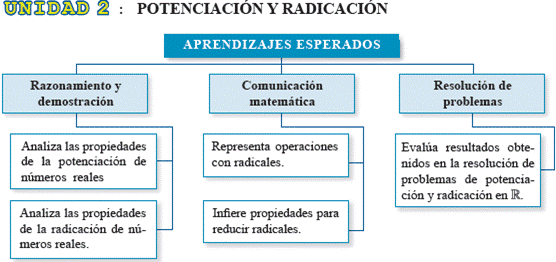

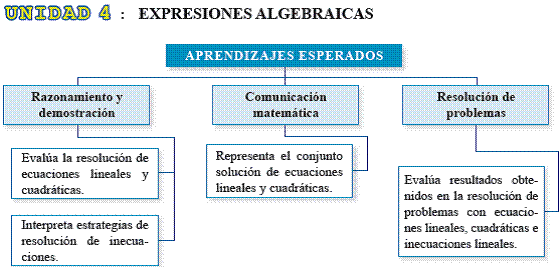
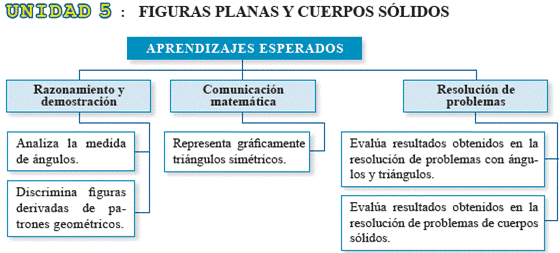
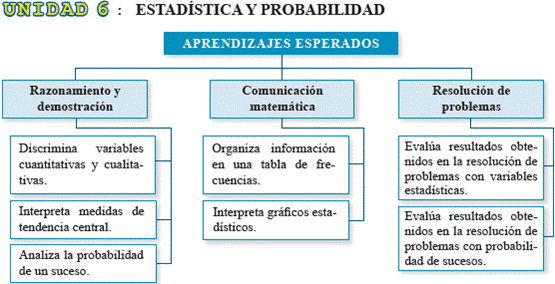
La función real de variable real f, cuya regla de correspondencia es
![]()
está definida para el conjunto de números reales no negativos.

La función raíz cuadrada f es una función creciente, es decir:
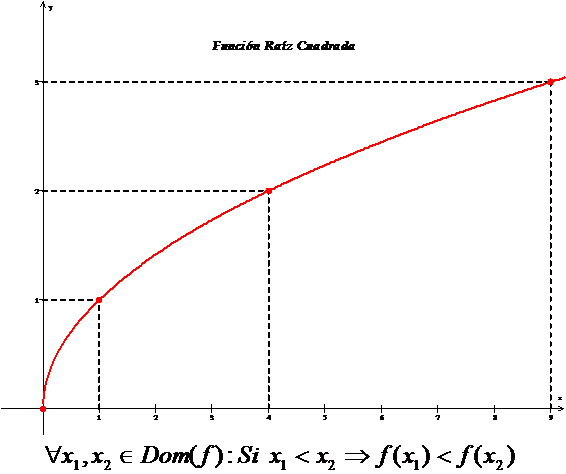
Aproximaciones e iteraciones: raíz cuadrada de a (a: no negativo)
1.1 Para representar al número irracional raíz cuadrada de dos se utiliza la notación:
![]()
![]()
se puede obtener, mediante iteraciones, el valor de la raíz cuadrada de a.
Así, si a = 2:
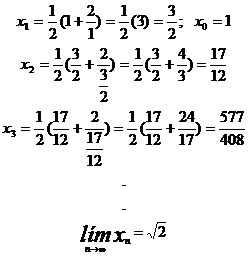
Por ejemplo, dada la gráfica:
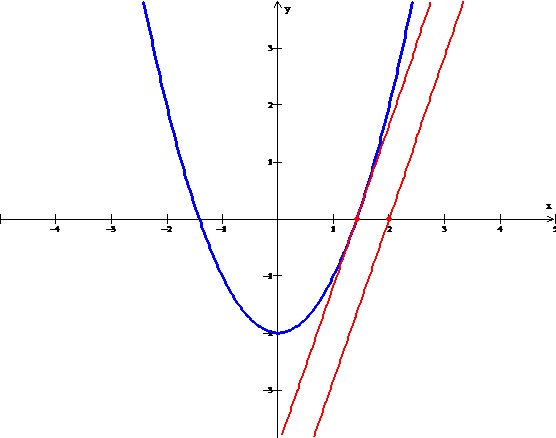
A partir de la gráfica, sea
![]()
entonces la fórmula de recurrencia es la siguiente:
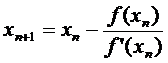
De donde,
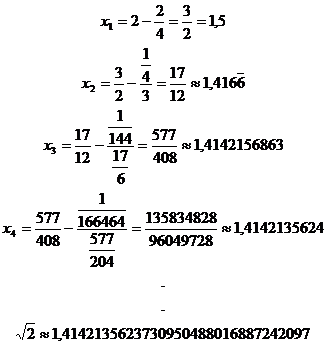
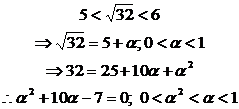
![]()
Geométricamente
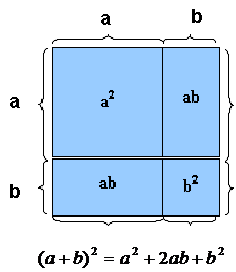
lo cual implica
![]()
Si la longitud del lado b es pequeña, entonces
![]()
haciendo h = 2ab:
![]()
En nuestro ejemplo:
![]() Sigue leyendo
Sigue leyendo
SITUACIONES PROBLEMAS
1.1 Estrategia de solución de la situación problema
Paso 01: Estandarizar

Paso 02: Introducir valores para z en WINSTATS
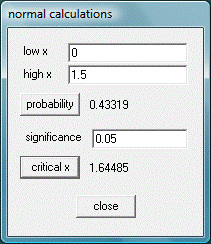
Paso 03: Área bajo la curva normal con WINSTATS
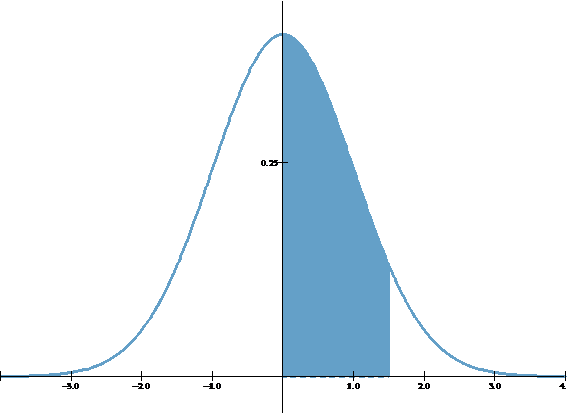
1.2 Respuesta
2.1 Estrategia de solución de la situación problema
Paso 01: Estandarizar
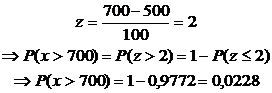
Paso 02A: Introducir valores para z en WINSTATS
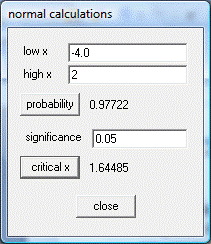
Paso 03A: Área bajo la curva normal con WINSTATS
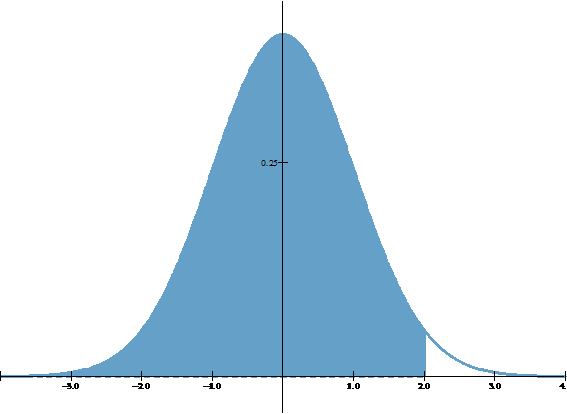
También, sin pérdida de generalidad, se puede afirmar que:
Paso 02B: Introducir valores para z en WINSTATS
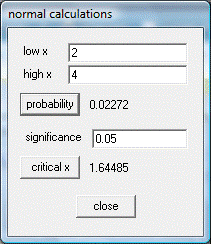
Paso 03B: Área bajo la curva normal con WINSTATS
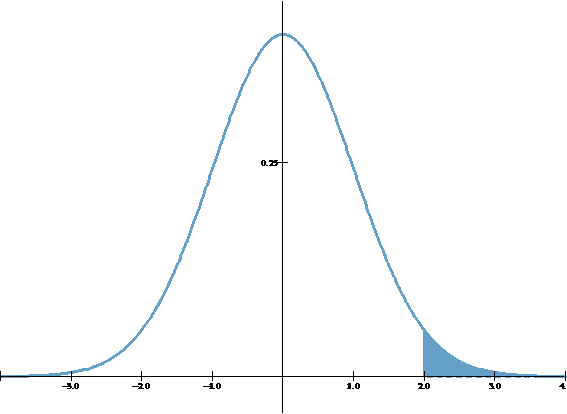
2.2 Respuesta