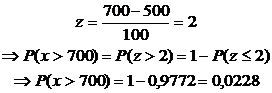Archivo de la categoría: Estadística: aproximación pedagógica

New category

Pisa 2009: Comprensión Lectora /Sexo

[Visto: 875 veces]

En un post anterior (9/12/10) se presentaron los resultados de Pisa 2009. A continuación se presentan las calificaciones promedio (mean score) por país miembro de la OCDE de la prueba de Comprensión Lectora, según sexo (Mean scores and gender differences in PISA 2009). Como se puede verificar en la data se ha incluido los puntajes promedios de Brasil, Indonesia y Federación Rusa.

En la presentación de las puntuaciones se ha utilizado tres software: Winstats, InfoStat y Spss.

Winstats

InfoStat

Spss

PD: Los resultados del total de países participantes los puede encontrar aquí.

Sigue leyendo →

Exploración de datos con Winstat (parte IV):

Deja una respuesta

[Visto: 1233 veces]

Diagrama dispersión (Muestra: n = 2 000)

Variable independiente: Altura

Variable independiente: Peso

Diagrama dispersión – SPSS (Muestra: n = 2 000)

Variable independiente: Altura

Variable independiente: Peso
Sigue leyendo →

Exploración de datos con Winstat (parte III):

Deja una respuesta

[Visto: 843 veces]

Total – Peso (Muestra: n = 2 000)

Frecuencia relativa:

Frecuencia acumulada:

Box-plot:

Restricción – Mujeres (Muestra: n = 1 000)

Frecuencia relativa:

Box-plot:

Restricción – Hombres (Muestra: n = 1 000)

Frecuencia relativa:

Box-plot:

SPSS – Total

SPSS – Box Plot (Sexo)

Sigue leyendo →

Exploración de datos con Winstat (parte II):

Deja una respuesta

[Visto: 1260 veces]

Total – Altura (Muestra: n = 2 000)

Frecuencia relativa:

Frecuencia acumulada:

Box-plot:

Restricción – Mujeres (Muestra: n = 1 000)

Frecuencia relativa:

Box-plot:

Restricción – Hombres (Muestra: n = 1 000)

Frecuencia relativa:

Box-plot:

SPSS – Total

SPSS – Box Plot (Sexo)

Sigue leyendo →

Exploración de datos con Winstat (parte I):

Deja una respuesta

[Visto: 1284 veces]

Como ya se ha presentado en artículos anteriores, el software libre Winstat es un software estadístico de fácil uso (¡se puede “llevar” en un USB!).

Existen en el mercado editorial muy buenos libros tutoriales para aprender a utilizar software estadístico; quizá el software estadístico más conocido sea el SPSS el cual necesita licencia. Un tutorial recomendable es IBM SPSS statistics 19 de Collin D. Gray y Paul R. Kinnear, publicado este año por Psychology Press. Información detallada la pueden encontrar en www.psypress.com

Los softwares estadísticos compilan información a partir de una base de datos. Por ejemplo en Excel la extensión de la base de datos es *.xls; en Spss la extensión es *.sav; en Minitab la extensión es *.mpj y en Winstat la extensión es *.fma

A continuación presentamos un conjunto de resultados obtenidos con el Winstat a partir de una muestra de dos mil personas según estatura (en centímetros), peso (en kilogramos), sexo (masculino, femenino) y tipo de sangre (factor Rh). Los resultados obtenidos se han contrastado con los procesados por el software Spss.

Muestra: n = 2 000

SPSS:

Peso – Altura:

Restricción (hombres):

Restricción (mujeres):

Restricción (Spss – sexo):

Sigue leyendo →

Distribuciones de Probabilidad con WINSTAT (parte II): Área bajo la curva

Deja una respuesta

[Visto: 3638 veces]

1. Ji – cuadrado (situación problema)

Si la variable X se distribuye Normalmente y si extraemos una m.a.s. de 12 observaciones, las cuales tipificamos, las elevamos al cuadrado y las sumamos; cuánto valen las probabilidades de que esa suma sea:

a) Menor que 14,845

De la gráfica, observamos que si la probabilidad mayor que 14,845 es 0,25004 entonces, por complemento, la respuesta es 0,74996.

b) Mayor que 6,4

Verificando respuesta ítem b en la tabla:

2. t de Student (situación problema)

Si la variable X se distribuye según el modelo t de Student con 14 grados de libertad, calcule la probabilidad de obtener valores menores que 0,537:

De la gráfica, observamos que si la probabilidad mayor que 0,537 es 0,29985 entonces, por complemento, la respuesta es 0,70015.

Se adjunta Tabla con otros valores calculados:

* Ejemplos tomados de Problemas y Ejercicios de Psicoestadística (autores: Botella, J. y Barriopedro. M. – Ed. Pirámide, 1994)

Sigue leyendo →

Distribuciones de Probabilidad con WINSTAT (parte I): Área bajo la curva

Deja una respuesta

[Visto: 1535 veces]

1. Normal: X ~ N(30, 10)

1.1 P( 21 < x < 46) = 0.7611

1.2 P( 18 < x < 28) = 0.3057

1.3 P( 39.4 < x < 49.5) = 0.1480

2. Binomial (Situación problema):

2.1 Si un estudiante responde al azar una prueba de 10 preguntas de tipo verdadero/falso, conteste las siguientes preguntas, definiendo X como “número de aciertos”.
a) Obtener el valor esperado y la varianza de X:

b) ¿Cuál es la probabilidad de que acierte 4?
c) ¿Cuál es la probabilidad de que acierte 5?
d) ¿Cuál es la probabilidad de que acierte 7 o más?
e) ¿Cuánto vale F(2)?

Respuestas (b, c, d, e) en la tabla adjunta:

2.2 En el contexto de la situación problema anterior conteste las mismas preguntas pero considerando que el número de alternativas para cada pregunta sea de 5 (de las cuales solo una es correcta):

a) Obtener el valor esperado y la varianza de X:

b) ¿Cuál es la probabilidad de que acierte 4?
c) ¿Cuál es la probabilidad de que acierte 5?
d) ¿Cuál es la probabilidad de que acierte 7 o más?
e) ¿Cuánto vale F(2)?

Respuestas (b, c, d, e) en la tabla adjunta:

* Ejemplos tomados de Problemas y Ejercicios de Psicoestadística (autores: Botella, J. y Barriopedro. M. – Ed. Pirámide, 1994)

Sigue leyendo →

DISTRIBUCIÓN NORMAL: ÁREAS CON WINSTATS

Deja una respuesta

[Visto: 6995 veces]

SITUACIONES PROBLEMAS

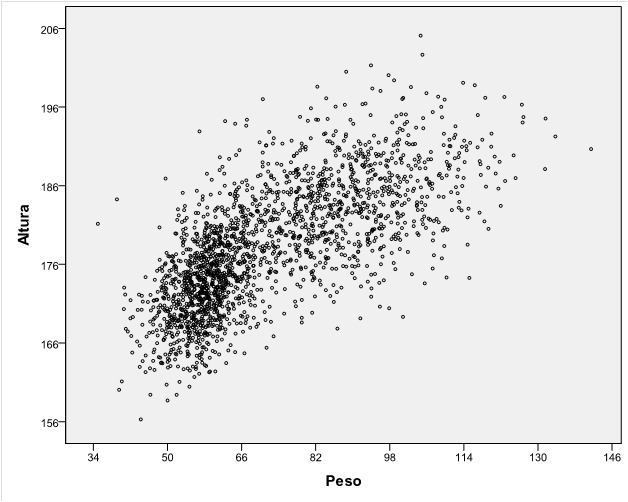
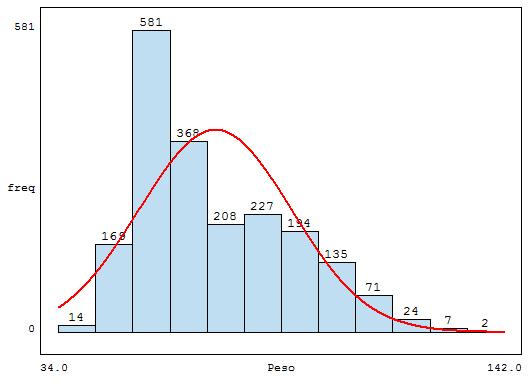
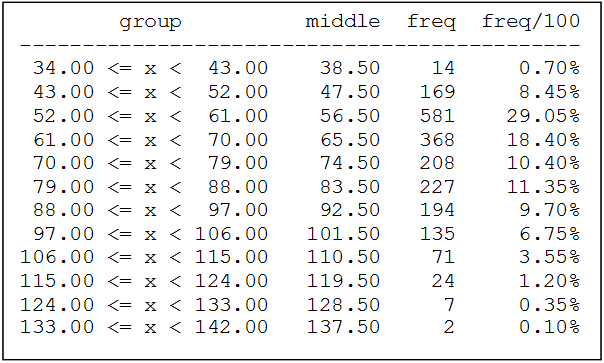
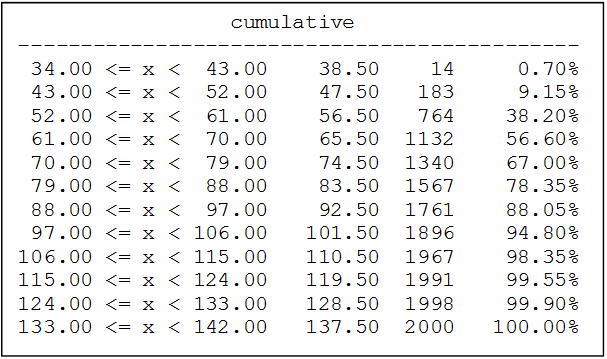
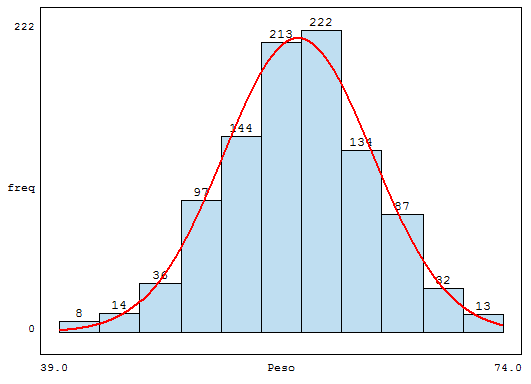
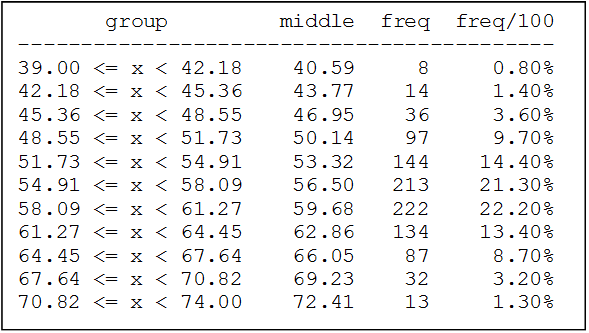
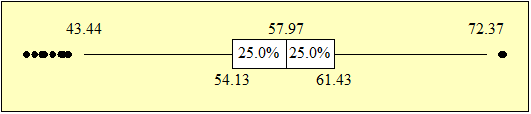
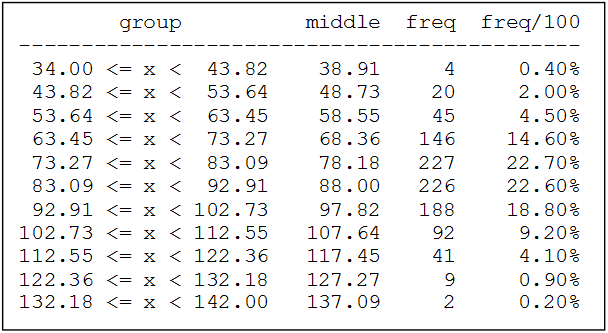
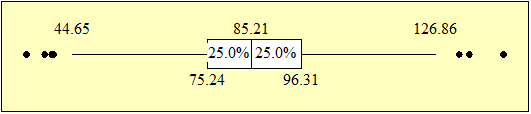
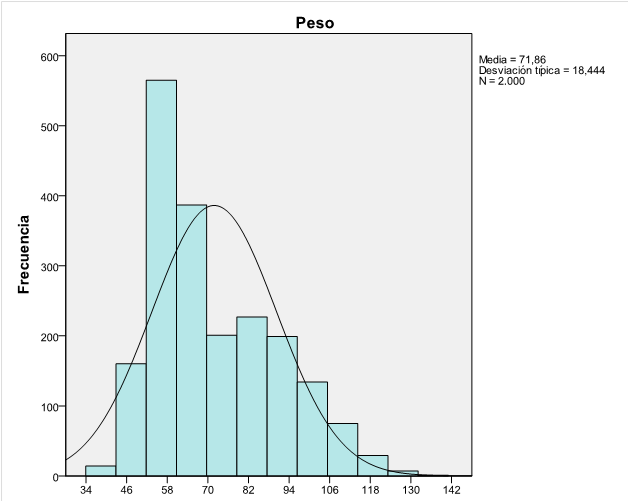
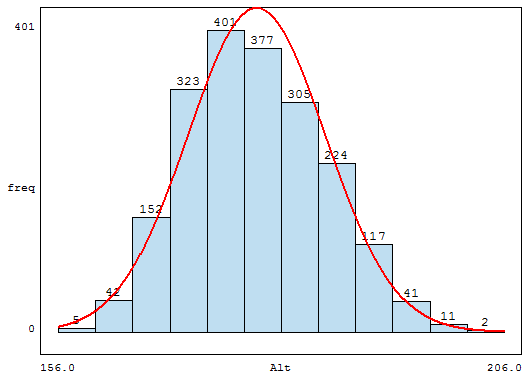
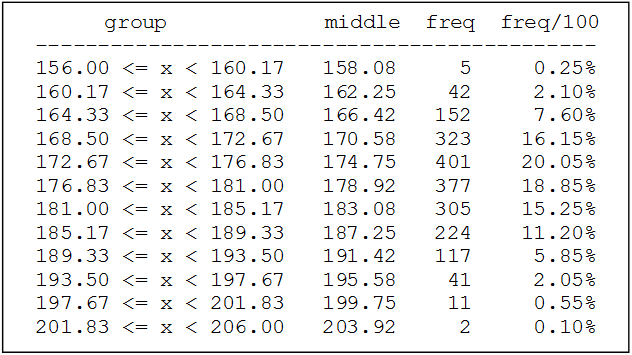
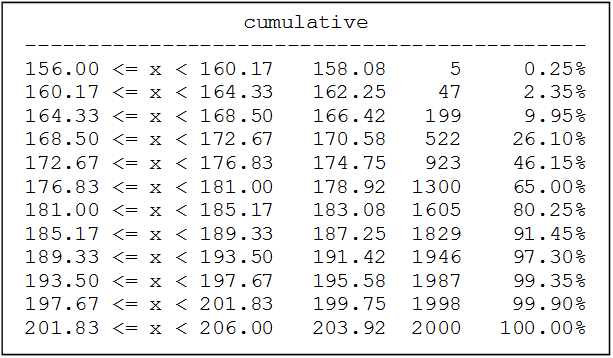
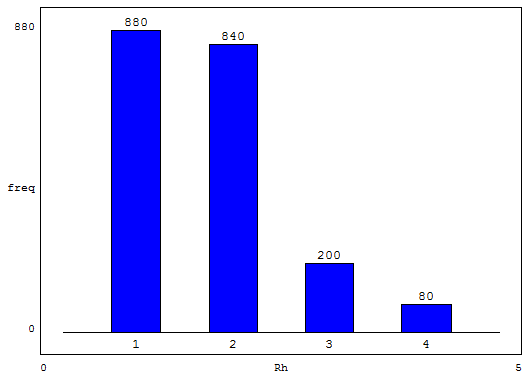
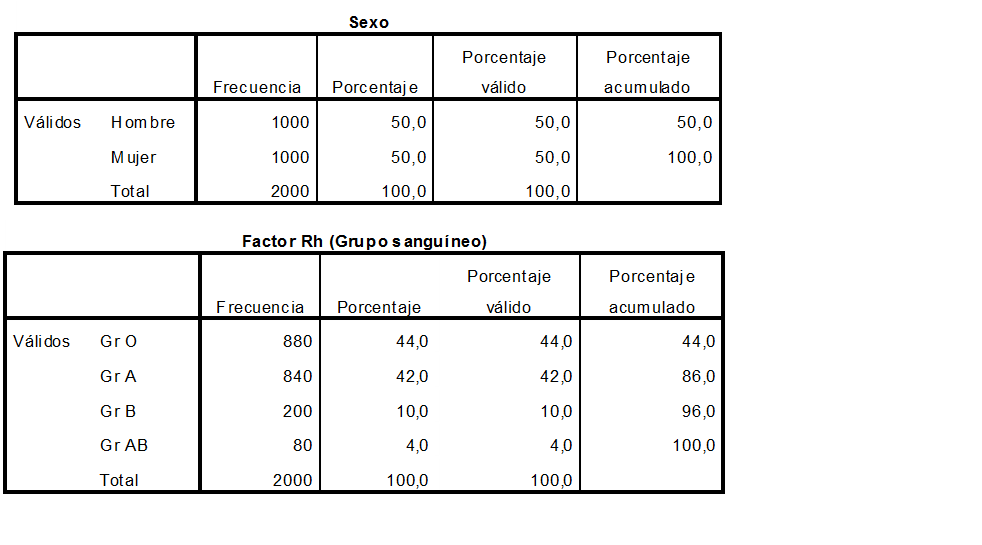
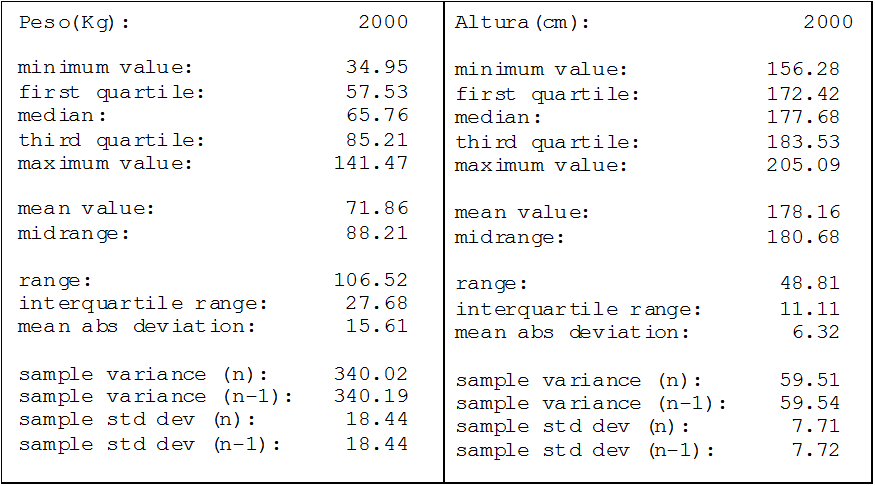
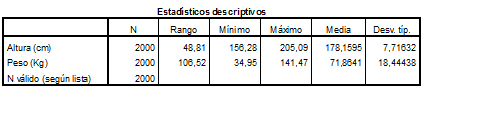
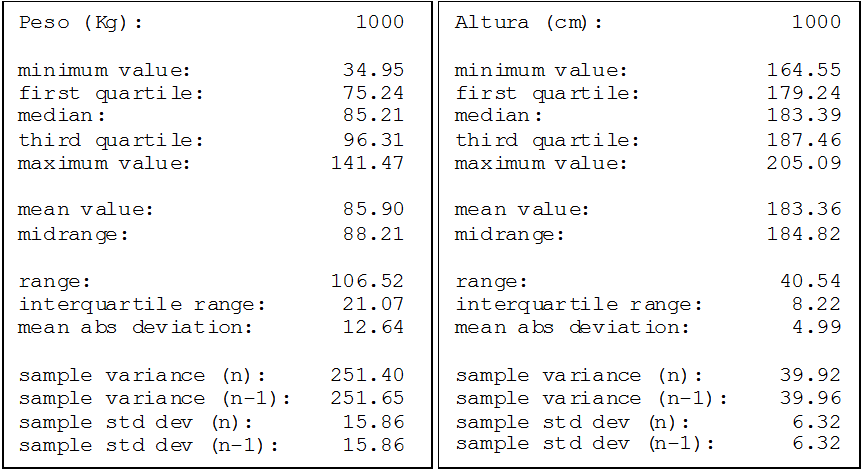
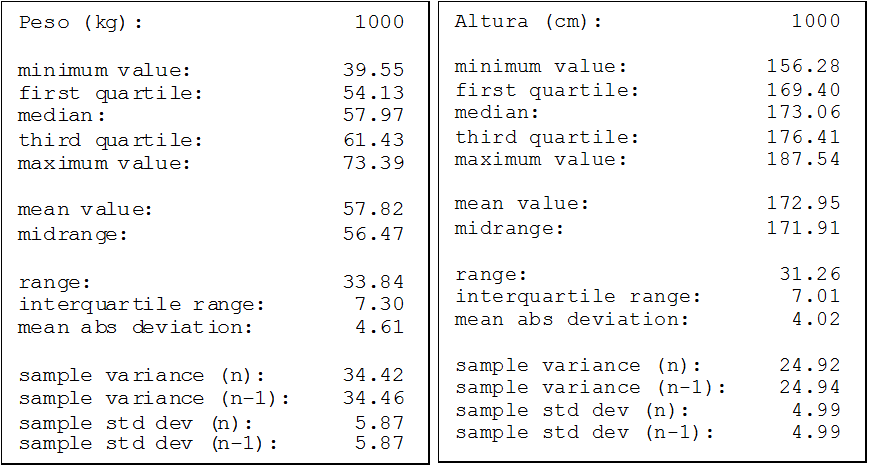
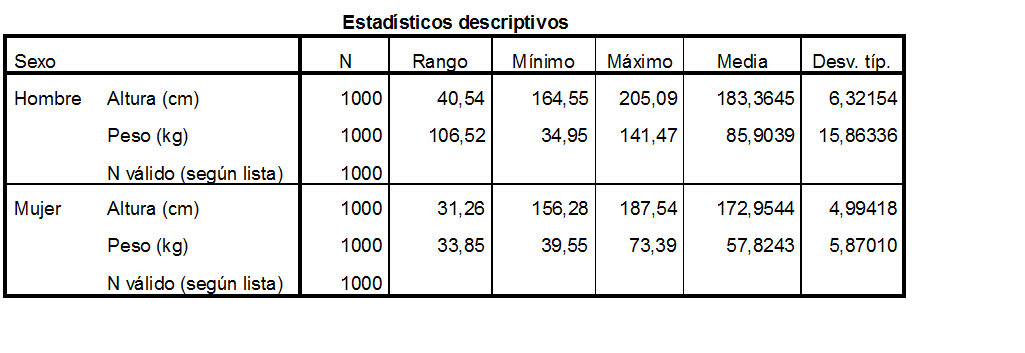
Una empresa textil implementa un programa de capacitación con el objetivo de optimizar las habilidades procedimentales de los supervisores técnicos del Área de Producción. Teniendo en cuenta los ritmos de aprendizaje de cada supervisor del área de producción y que la capacitación se realiza a través de tres módulos en un entorno virtual, en consecuencia, cada supervisor necesitará un número de horas diferente para culminar los tres módulos. El Área de Recursos Humanos ha compilado información de capacitaciones anteriores y ha reportado que el tiempo promedio para completar la capacitación, a través de los tres módulos, es de 500 horas y que esta variable aleatoria distribuida normalmente tiene una desviación estándar de 100 horas.

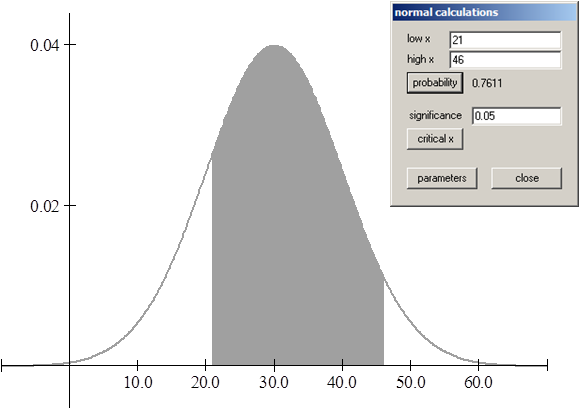
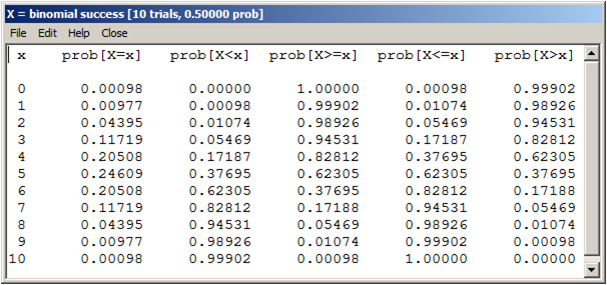
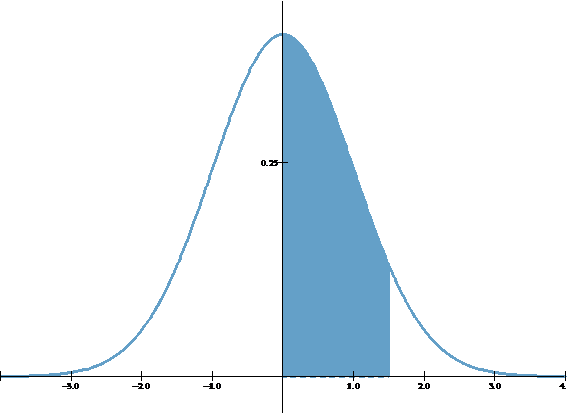
1. ¿Cuál es la probabilidad de que un supervisor técnico, elegido al azar, emplee entre 500 y 650 horas para cubrir los tres módulos del programa de capacitación?

1.1 Estrategia de solución de la situación problema

Paso 01: Estandarizar

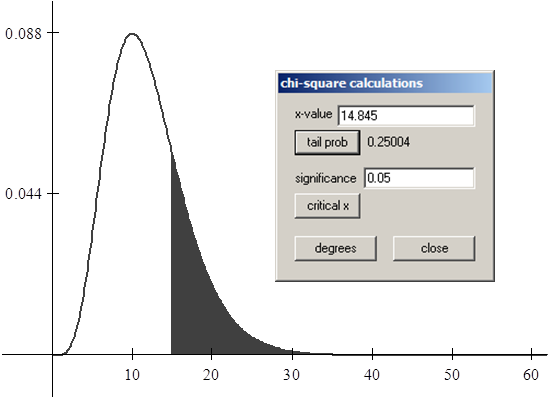
Paso 02: Introducir valores para z en WINSTATS
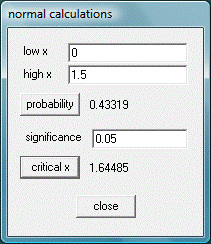
z_normal

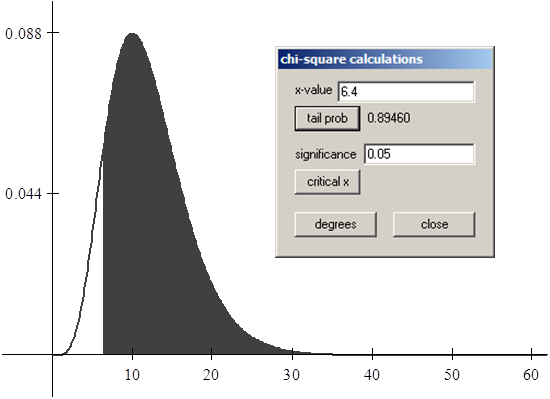
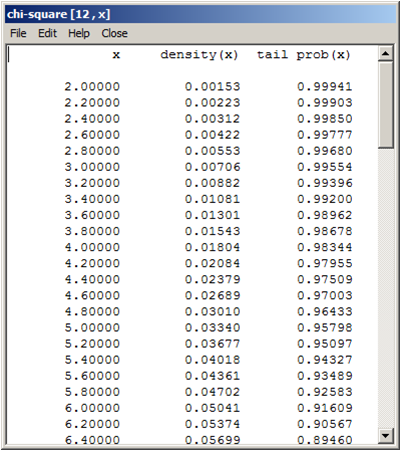
Paso 03: Área bajo la curva normal con WINSTATS
graf_normal

1.2 Respuesta

La probabilidad de que un supervisor técnico, elegido al azar, emplee entre 500 y 650 horas para cubrir los tres módulos del programa de capacitación es – aproximadamente – 0,4332.

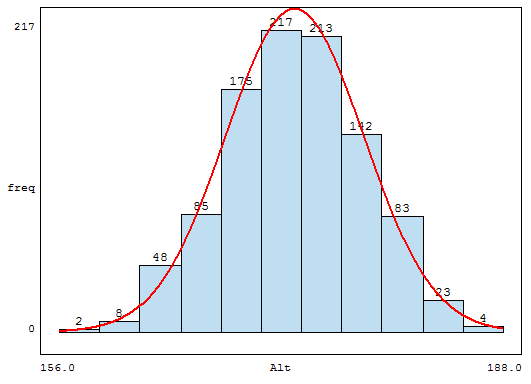
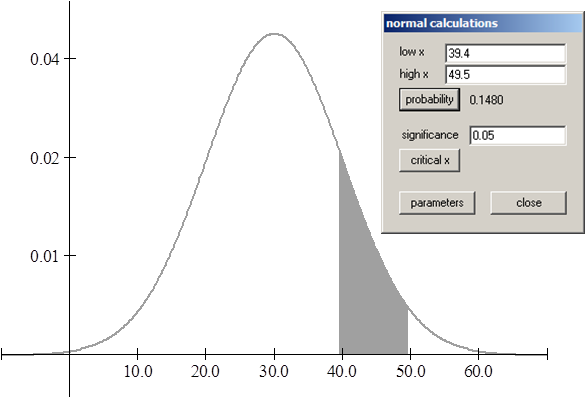
2. ¿Cuál es la probabilidad de que un supervisor técnico, elegido al azar, emplee más de 700 horas para cubrir los tres módulos del programa de capacitación?

2.1 Estrategia de solución de la situación problema

Paso 01: Estandarizar
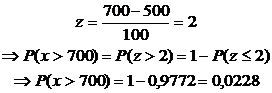
fig2.1

Paso 02A: Introducir valores para z en WINSTATS
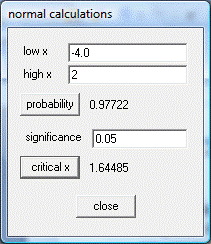
fig2.2

Paso 03A: Área bajo la curva normal con WINSTATS
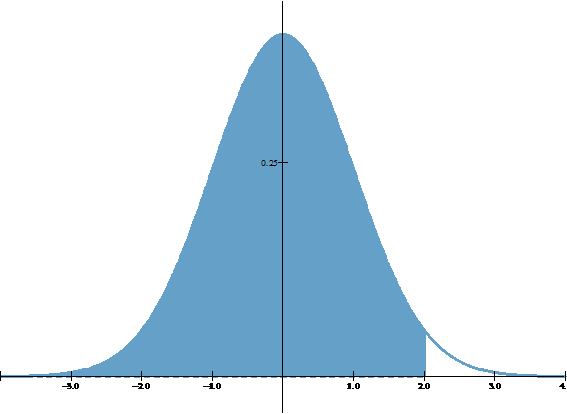
fig2.3

También, sin pérdida de generalidad, se puede afirmar que:

Paso 02B: Introducir valores para z en WINSTATS
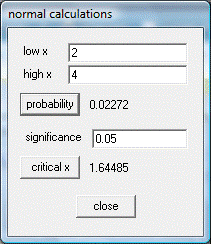
fig2.4

Paso 03B: Área bajo la curva normal con WINSTATS
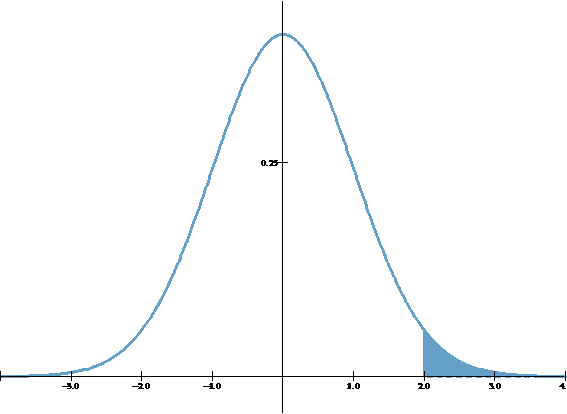
fig2.4

2.2 Respuesta

La probabilidad de que un supervisor técnico, elegido al azar, emplee más de 700 horas para cubrir los tres módulos del programa de capacitación es – aproximadamente – 0,023.

Sigue leyendo →

ESTADÍSTICA DESCRIPTIVA BIDIMENSIONAL: diagramas de dispersión con MiniTab (parte III)

Deja una respuesta

[Visto: 7489 veces]

Bajo el mismo supuesto de la parte I, teniendo en cuenta que las variables son cuantitativas, se presentan los resultados obtenidos con el MiniTab:

ASOCIACIÓN MADRE – HIJO

NUBE DE PUNTOS y BOX PLOT