Archivo por meses: junio 2012
Distribuciones de Probabilidad con WINSTAT (parte II): Área bajo la curva
Si la variable X se distribuye Normalmente y si extraemos una m.a.s. de 12 observaciones, las cuales tipificamos, las elevamos al cuadrado y las sumamos; cuánto valen las probabilidades de que esa suma sea:
a) Menor que 14,845
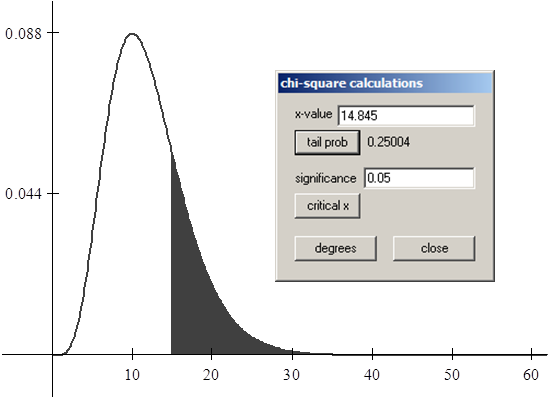
b) Mayor que 6,4
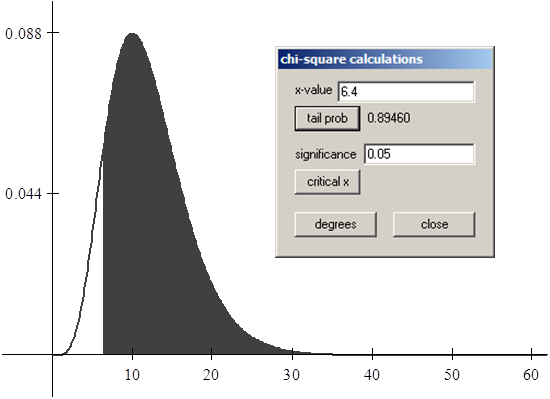
Verificando respuesta ítem b en la tabla:
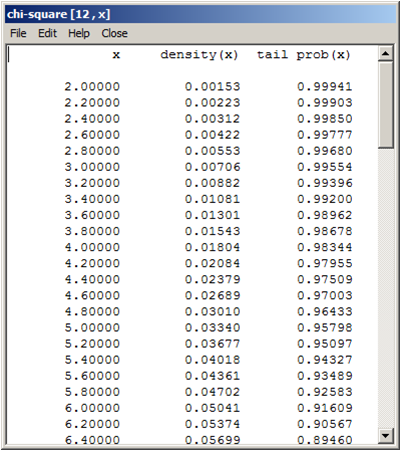
Si la variable X se distribuye según el modelo t de Student con 14 grados de libertad, calcule la probabilidad de obtener valores menores que 0,537:
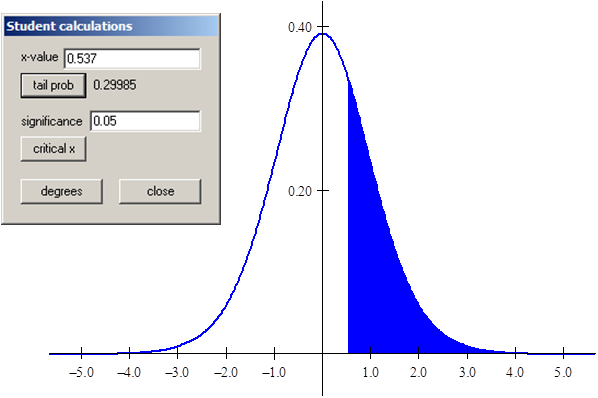
Se adjunta Tabla con otros valores calculados:
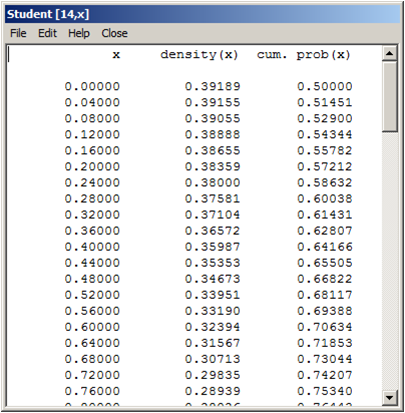
Distribuciones de Probabilidad con WINSTAT (parte I): Área bajo la curva
1. Normal: X ~ N(30, 10)
1.1 P( 21 < x < 46) = 0.7611
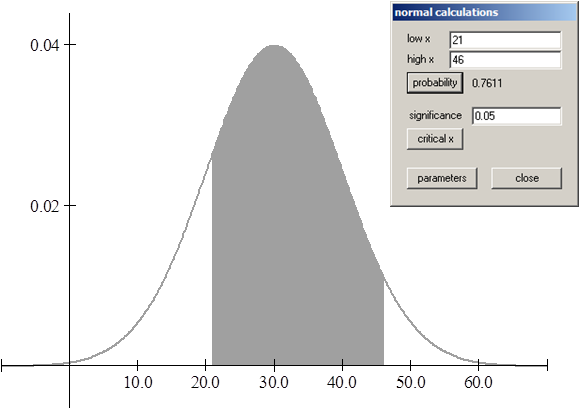
1.2 P( 18 < x < 28) = 0.3057
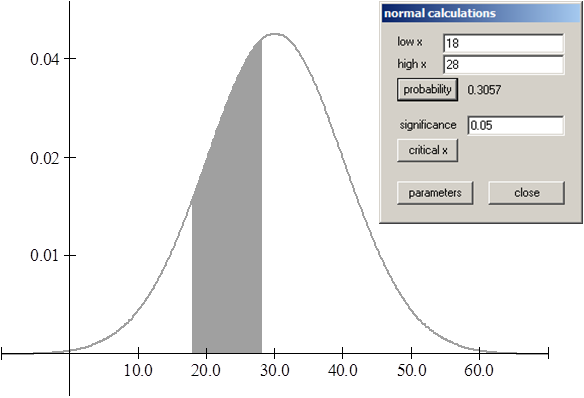
1.3 P( 39.4 < x < 49.5) = 0.1480
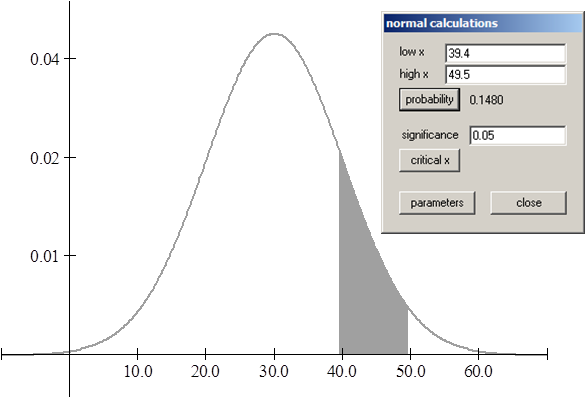
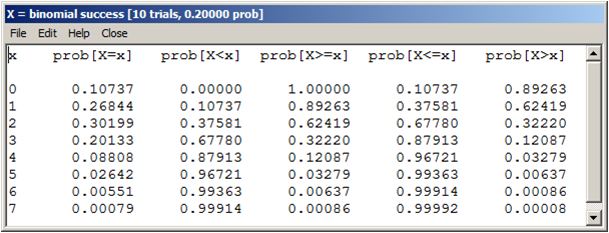
2.1 Si un estudiante responde al azar una prueba de 10 preguntas de tipo verdadero/falso, conteste las siguientes preguntas, definiendo X como “número de aciertos”.
a) Obtener el valor esperado y la varianza de X:
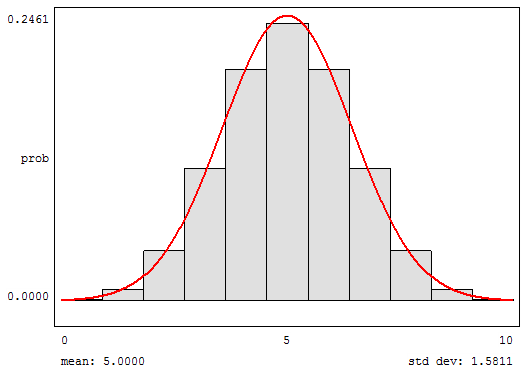
b) ¿Cuál es la probabilidad de que acierte 4?
c) ¿Cuál es la probabilidad de que acierte 5?
d) ¿Cuál es la probabilidad de que acierte 7 o más?
e) ¿Cuánto vale F(2)?
Respuestas (b, c, d, e) en la tabla adjunta:
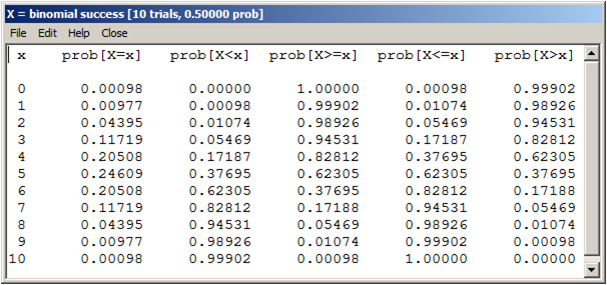
a) Obtener el valor esperado y la varianza de X:
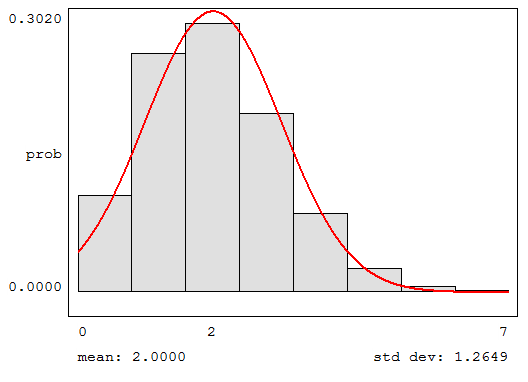
b) ¿Cuál es la probabilidad de que acierte 4?
c) ¿Cuál es la probabilidad de que acierte 5?
d) ¿Cuál es la probabilidad de que acierte 7 o más?
e) ¿Cuánto vale F(2)?
Respuestas (b, c, d, e) en la tabla adjunta: