[Visto: 20192 veces]
La función real de variable real f, cuya regla de correspondencia es
![]()
está definida para el conjunto de números reales no negativos.
La notación algebraica se utiliza para representar al número real raíz cuadrada de x, x no negativo:

La función raíz cuadrada f es una función creciente, es decir:
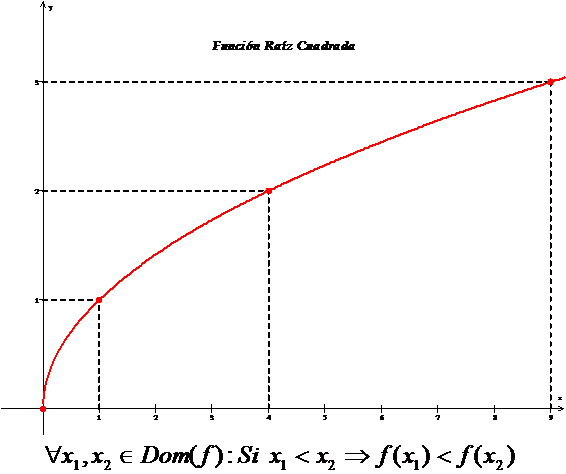
Aproximaciones e iteraciones: raíz cuadrada de a (a: no negativo)
1.1 Para representar al número irracional raíz cuadrada de dos se utiliza la notación:
![]()
Existen varias maneras de aproximar este valor; por ejemplo, a partir de la fórmula de recurrencia (atribuida a Herón de Alejandría):
![]()
se puede obtener, mediante iteraciones, el valor de la raíz cuadrada de a.
Así, si a = 2:
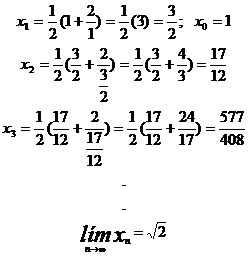
1.2 También, para hallar el valor del número real raíz cuadrada de dos podemos hacer uso del Método de Newton de Aproximaciones Sucesivas, teniendo en cuenta que existen algunas condiciones iniciales para su aplicación. Es importante tener en cuenta que no siempre el Método de Newton genera aproximaciones que convergen hacia la raíz que se desea encontrar, una dificultad es que el valor inicial x(0) no esté suficientemente cerca de la raíz a encontrar, para iniciar el proceso de convergencia; otra dificultad surge cuando la función derivada de f es cero en la raíz o cerca de la raíz, dado que la derivada de f se encuentra en el denominador del algoritmo (ver fórmula de recurrencia).
Por ejemplo, dada la gráfica:
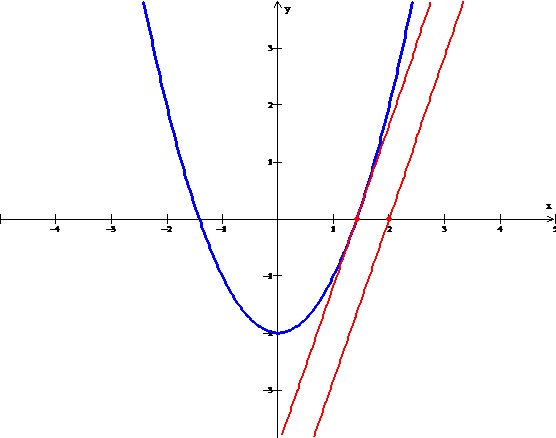
A partir de la gráfica, sea
![]()
entonces la fórmula de recurrencia es la siguiente:
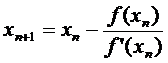
De donde,
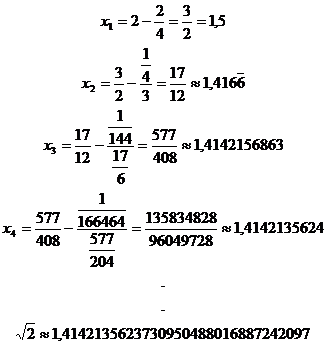
De lo expuesto en 1.1 como en 1.2, utilizando una calculadora y ejecutando el comando cuyo rótulo es sqrt (o la notación algebraica de raíz cuadrada) se puede comprobar o verificar sendos resultados
Obviamente, surge una interrogante: ¿Para qué utilizar estos procedimientos si existe la calculadora? Bueno, si bien es cierto que actualmente se puede conocer, presionando un botón, el valor de la raíz cuadrada de a, a no negativo; haciendo un poco de memoria ¿cómo hicieron las civilizaciones antiguas para obtener una aproximación de estos números irracionales?
1.3 El Antiguo Imperio Babilónico se desarrolló en Mesopotamia entre los años 1900 A.C. y 1600 A.C. Existen, en la actualidad, tabletas cuneiforme de arcilla fielmente resguardadas en museos de universidades de prestigio a nivel mundial (por ejemplo la Colección Babilónica de la Universidad de Yale). La notación cuneiforme expresa números en base sexagesimal. Los babilonios resolvían, de manera natural a partir de un conjunto de tablas de sumas de cuadrados y cubos, ecuaciones de grado dos y grado tres. Sin embargo, resulta interesante cómo es que los babilonios hallaban una buena aproximación a la raíz cuadrada de un número dado. Se asume que los babilonios utilizaban un algoritmo similar al de Herón de Alejandría; es decir, empezaban por una aproximación inicial x(0).
Por ejemplo, para hallar la raíz cuadrada de 32, a partir de la gráfica de la función raíz cuadrada es fácil ver que
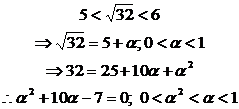
Sin pérdida de generalidad, despreciando el valor de alfa al cuadrado, obtenemos
![]()
Por lo tanto, una primera aproximación a la raíz cuadrada de 32 es 5+0,7=5,7.
Geométricamente
Se observa que el área de la región cuadrada “grande” equivale a la suma de las áreas de las regiones interiores:
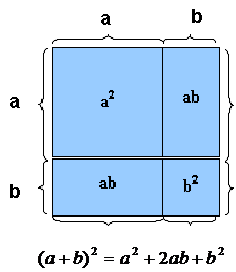
lo cual implica
![]()
Si la longitud del lado b es pequeña, entonces
![]()
haciendo h = 2ab:
![]()
En nuestro ejemplo:
![]() Sigue leyendo
Sigue leyendo