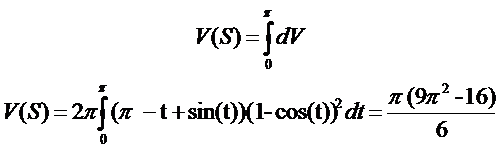[Visto: 6476 veces]
Longitud del arco de una curva
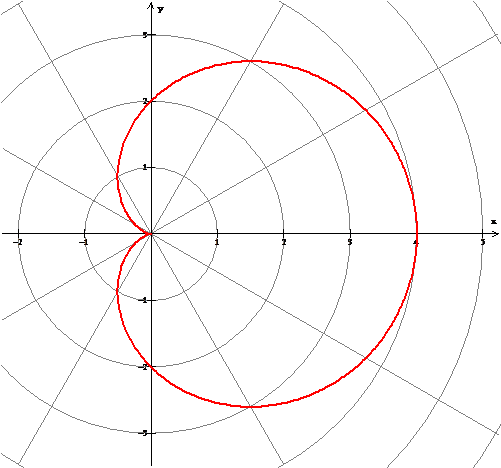
Ejemplo: Dada la cardiode p(t) = 2 (1 + cos(t)), si nos piden hallar la longitud del arco de dicha curva, ¿qué tenemos que hacer con el Winplot?
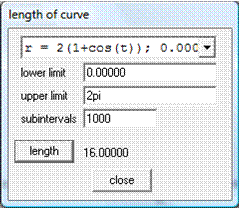
Primero, seleccionamos la ventana One, a continuación la opción Measurement, luego Arc Length… y aparece el recuadro length of curve. En este recuadro, digitamos 0 en lower limit y 2pi en upper limit. Finalmente, para obtener el valor de la longitud del arco de dicha curva, hacemos clic sobre length y nos da el resultado: 16 (ver recuadro adjunto)
Si se desea verificar la respuesta, observamos que la gráfica de la cardiode es simétrica respecto del eje X; cuando t varía desde t = 0 hasta t = pi, el radio vector recorre el arco superior de la curva. Dado que p(t) = 2 (1 + cos(t)), entonces:
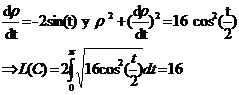
Sólidos de Revolución
A continuación se presentan dos ejemplos a partir de la figura acotada por un arco completo de la cicloide
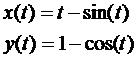
y el eje X.
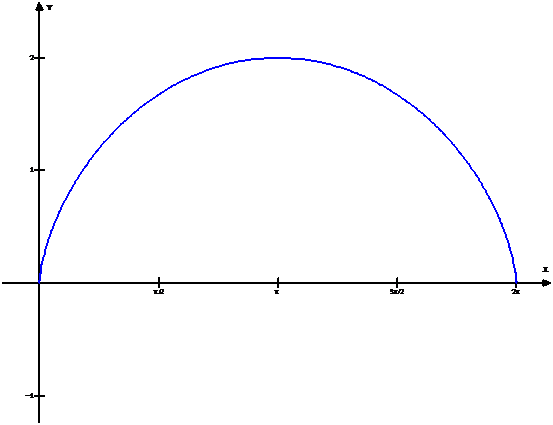
Ejemplo 01: Volumen del sólido de revolución
Si nos piden calcular el volumen del sólido formado por rotación de la figura acotada por un arco completo de la cicloide

y el eje X, alrededor del eje de simetría de la figura, lo que tenemos que hacer es seleccionar la ventana One, luego la opción Measurement, a continuación Volume of revolution … y aparece el recuadro volume of revolution. En este recuadro, debajo de axis ax + by = c, digitamos los valores a = 1, b = 0, c = pi, arc start = 0, arc stop = pi. Finalmente, para hallar el volumen del sólido de revolución, hacemos clic sobre volume y nos da el valor aproximado: 38,13183
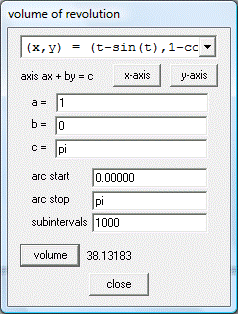
Si se opta por el cálculo infinitesimal, notamos que el eje de simetría de la figura es la recta x = pi, por lo que el volumen del tubo cilíndrico obtenido por rotación (alrededor de esta recta) del rectángulo de la figura es dV = 2pi(pi – x)y dx:
De donde: