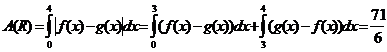1. Preliminares
La enseñanza de la matemática, en un grueso de instituciones educativas de educación básica y superior, sigue siendo una enseñanza tradicional de carácter expositivo, de allí que se hace necesario e indispensable que los docentes de matemática incorporen los softwares – en particular los software libres o gratuitos – como herramientas o recursos pedagógicos que favorecen un aprendizaje por descubrimiento y el trabajo en equipo, en las sesiones de clase, en el marco de una metodología activa. Hay que destacar la utilidad del software como herramienta de verificación de resultados y como fuente de experimentación que permita al estudiante elaborar sus conjeturas, contrastarlas y avanzar en la resolución de una situación problemática.
Cabe precisar que la introducción de las Tecnologías de la Información y de la Comunicación en el área de matemática de la educación básica y superior generan en el docente una serie de interrogantes: ¿De qué manera, en qué momento y cómo se van a introducir las nuevas tecnologías en las sesiones de clase? ¿Existe material bibliográfico referente a la incorporación de las nuevas tecnologías? ¿Se cuenta con la infraestructura idónea? En esta línea, hace once años, De Moura Castro en “La Educación en la Era de la Informática” (New York: B.I.D., 1998, p.121) propuso que:
“La educación debe cambiar a fin de preparar debidamente a los ciudadanos del futuro para funcionar en una sociedad en cambio continuo. Por consiguiente, es necesario reemplazar el paradigma actual de la educación (la producción masiva de ciudadanos con conocimientos prefabricados y títulos que los habilitan para una larga carrera) con modelos pedagógicos que doten a los ciudadanos de aptitudes para aprender durante toda la vida en una sociedad en la cual las tecnologías de la comunicación y la información son uno de los pilares de la infraestructura”.
2. Tópicos de cálculo integral
A continuación, a manera de ejemplo, se presenta la aplicación del Winplot en tópicos de cálculo integral en el plano:
Área de una región en el plano
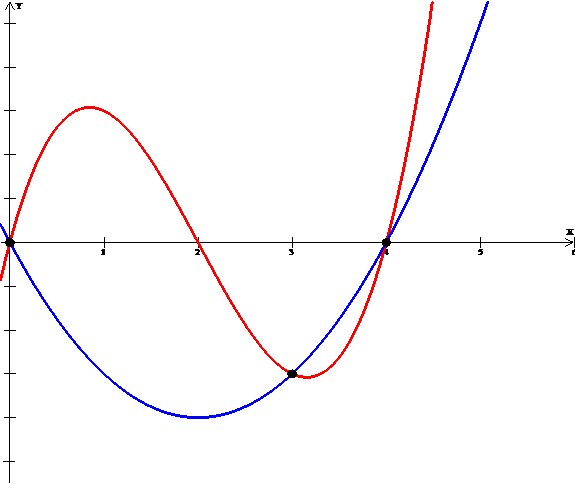
Ejemplo: Si queremos encontrar el área de la región acotada por las curvas f(x) = x^3- 6x^2+ 8x y g(x) = x^2 – 4x.
El valor de dicha área es dado por la integral definida de la función |f(x) – g(x)|, con límite inferior igual a 0 y límite superior igual a 4, es decir:
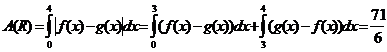
Con el Winplot seleccionamos la ventana Two, luego hacemos clic sobre la opción Integrate, a continuación aparece el recuadro integrate f-g. En este recuadro digitamos, primero, los límites inferior (lower limit = 0) y superior (upper limit = 3). A continuación, seleccionamos un método de integración (por ejemplo midpoint) para obtener el valor del área de la región acotada por las curvas f(x), g(x) y las rectas x = 0 y x = 3. Si, además, se desea pintar la región en mención seleccionamos overlay y hacemos clic sobre definite.
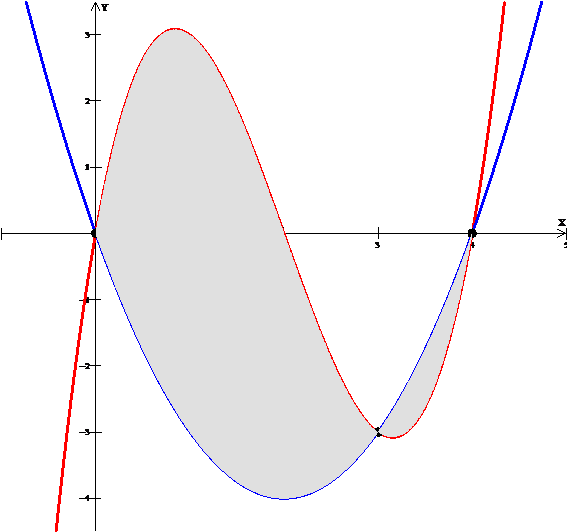
Obsérvese que en la pantalla del monitor aparece cubierta o pintada la región pedida y en el recuadro integrate f-g aparece el valor aproximado del área: 11,25001.
Tener en cuenta que para calcular el área de la región acotada por las curvas g(x), f(x) y las rectas x = 3 y x = 4, en el recuadro integrate f-g, primero seleccionamos la regla de correspondencia y = x^2 – 4x y luego la regla de correspondencia y = x^3- 6x^2+ 8x. A continuación, digitamos los límites inferior (lower limit = 3) y superior (upper limit = 4); seleccionamos un método de integración (por ejemplo midpoint) para obtener el valor del área de la región acotada. Si se desea pintar la región en mención seleccionamos overlay y hacemos clic sobre definite. Obsérvese que en la pantalla del monitor aparece cubierta o pintada la región pedida y en el recuadro integrate f-g aparece el valor aproximado del área: 0,58333.
Por lo tanto: A(R) =11,25001 + 0,58333 =11,83334 (aprox.)