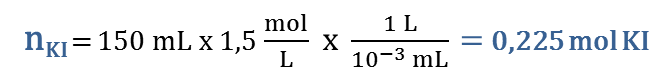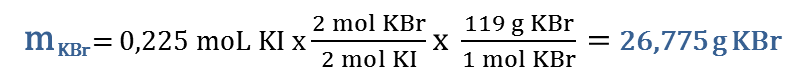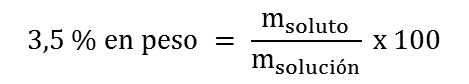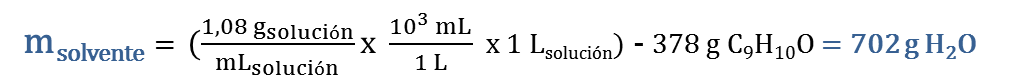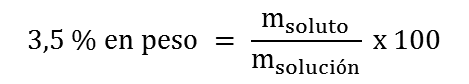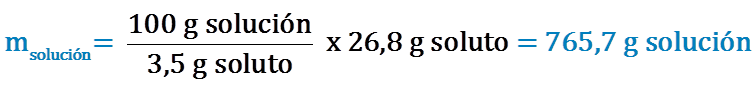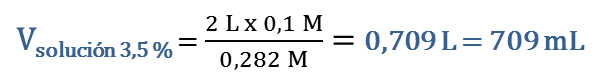Estequiometría y soluciones

Un forma de obtener I₂ sólido es a través de la reacción del bromo, Br₂, con solución acuosa de KI, según la  reacción:

Cuando trabajamos estequiometría, lo primero que debemos hacer es balancear la ecuación dada:

Br_2(l)   +   2 KI_(ac)     →     2 KBr_(ac)   +   I_2(s)

Luego calcularemos las moles disponibles de cada reactivo:

Ahora determinaremos quién es el reactivo limitante y quién el reactivo en exceso, para ello calculamos la cantidad de cada reactivo, que se necesitaría para que reaccionase todo el otro reactivo disponible:

           ⇒ KI es el reactivo limitante

     ⇒ Br₂ es el reactivo en exceso

Conocido el reactivo limitante, procedemos a determinar la cantidad del producto solicitado, haciendo uso de los factores estequiométricos:

El aceite de cinamon, obtenido de las ramas y hojas de árboles de canela que crecen en las zonas tropicales, se utiliza en la producción de perfumes y cosméticos. Su constituyente principal es el aldehído cinámico, C₉H₈O, sin embargo una concentración elevada de éste ocasiona severas irritaciones en la piel, por lo que las concentraciones presentes en los perfumes deben ser bajas. Con la finalidad de evitar irritaciones en la piel se buscó un derivado del aldehído cinámico, de fórmula C₉H₁₀O, con propiedades similares, pero que no causa irritaciones a la piel. Éste se prepara haciendo reaccionar aldehído cinámico, C₉H₈O, con hidrógeno gaseoso, H₂, según la reacción:

C₉H₈O_(ac)   +   H_2(g)     →     C₉H₁₀O_(ac)

Para obtener el derivado, C₉H₁₀O, se hacen reaccionar 15 L de solución de aldehído cinámico 3,5 M con  30,7 moles de hidrógeno gaseoso. Determina lo siguiente:

1. La cantidad en gramos, qué se obtendrán del derivado C₉H₁₀O, considerando un rendimiento del 95 %.
2. El derivado se utiliza en soluciones acuosas al 3,5 % en peso, ¿cómo prepararías 1 L de esta solución? Indica los pasos y las cantidades requeridas. La densidad de la solución es 1,08 g/mL.
3. A partir de la solución anterior (al 3,5 % en peso) se quiere preparar 2 L de una solución de 0,1 M del derivado, ¿qué volumen de la solución se requerirá?

1. Primero, verificamos si la ecuación está balanceada:

C₉H₈O_(ac)   +   H_2(g)     →     C₉H₁₀O_(ac)

Luego determinamos las moles disponibles de cada uno de los reactivos:

En base a la estequiometría y las cantidades disponibles de los reactantes, determinamos que el reactivo limitante es el hidrógeno, H₂. Entonces podemos calcular las moles teóricas del producto que se formarán:  Considerando que el rendimiento es del 95 %, determinamos la masa obtenida del producto derivado:

2. Primero determinamos la masa del soluto, C₉H₁₀O, que se requiere para preparar 1 L de solución acuosa 3,5 % en peso:

Conocida la masa del soluto, determinamos la masa del disolvente:

Como la densidad del agua es 1 g/mL, los 702 g de agua equivalen a 702 mL de H₂O.

Finalmente, para preparar 1 L de la solución al 3,5 % en peso se deben pesar 378 g de C₉H₁₀O y disolverlos en 702 mL de agua.

3. Como sabemos, los problemas no tienen una única vía de solución, por lo que vamos a enfocar el problema desde dos puntos de vista.

Determinamos primero cuántas moles del soluto C₉H₁₀O deben estar contenidos en los 2 L de solución 0,1 M y luego qué masa le corrresponde:

Ahora calculamos qué masa de solución contiene la masa requerida, es decir, los 26,8 g del soluto:

Finalmente determinamos qué volumen de solución al 3,5 % en peso necesitamos:

Para resolver el problema por otra vía, determinamos la molaridad, M, de la solución al 3,5 % en peso:

Como  n_soluto = M x V     ⇒     n_{soluto al 3,5 %} = 0,282 M x V_{3,5 %}     y     n_{soluto 0,1 M} = 0,1 M x 2 L

Luego, como se trata de hacer una dilución, las moles de C₉H₁₀O requeridas de la solución al 3,5 % en peso o 0,282 M, serán las mismas que estarán presentes en la nueva solución 0,1 M, es decir,

n_{soluto en solución al 3,5 %} = n_{soluto en solución 0,1 M}

De donde determinamos el volumen de solución al 3,5 % en peso que se requiere para preparar la nueva solución 0,1 M: