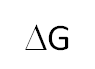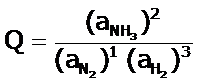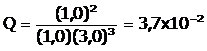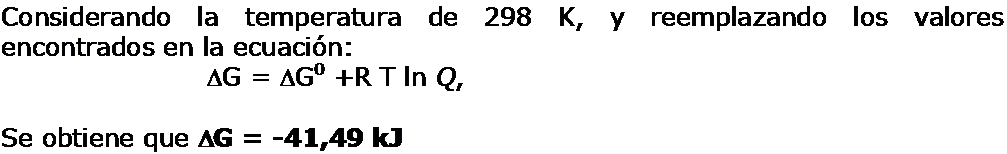1.7.1.- La Energía Libre de Gibbs y el Equilibrio Químico
Hasta ahora hemos estudiado la Energía Libre de Gibbs en condiciones estándares, el valor de esta variación nos permite predecir si la reacción ocurrirá o no, pero a las condiones estandar.
Pero la mayoría de las reacciones quimicas que se producen, tanto en los laboratorios como en la industria, no lo hacen en condiciones estándar.
Para poder explicar lo dicho en el parrafo anterior, vamos suponer los siguiente:
- La reacción quimica:
a A (ac) + bB(ac) → cC(ac) + dD(ac)
- Los reactivos se encuentran en solución acuosa y en estado estándar, lo que implica que, cada uno tiene una concentración 1M.
- Tan pronto se inicie la reacción la condición estandar deja de existir, pues los reactivos van a ir disminuyendo a medida que se irán formando los productos. Por lo tanto el cálculo de la Energía Libre de Gibbs a condición estándar ya no sería el adecuado y no podríamos predecir el sentido de la reacción.
Para situaciones en donde se pierde el estado estandar debemos calcular la variación de la energía Libre de Gibbs a condiciones diferentes del estándar.
donde:
- R es la constante de los gases expresada en términos de energía (8,314 J/K.mol)
- T es la temperatura de la reacción, en grados Kelvin
- Q es el cociente de reacción. Lineas abajo explicaremos que significa y como se determina el cociente de reacción.
Observa que en la ecuación anterior:
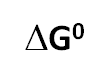es un valor constante,- RT Ln Q, no es un valor constante; la razón es que el cociente de reacción es función de la composición de la mezcla de reacción.
Para poder continuar debemos definir que se entiende por Cociente de Reacción y que se entiende por Actividad.
Q es el cociente de reacción:
Se define como el cociente entre las actividades de los productos, elevadas a sus índices estequiométricos y
las actividades de los reactantes elevadas a sus índices estequiométricos.
Teniendo como ejemplo la reacción química:
a A(ac) + b B(ac) → c C(ac) + d D(ac)
Podemos escribir el cociente de reacción (Q), como:
Actividad
La actividad, es un artificio matemático que permite tener un valor numérico adimensional (no tiene unidades).
Se obtiene al referir la condición de la sustancia, con un estado referencial. Éste estado está definido por la fase de la sustancia.
Por lo tanto, la actividad es el cociente entre el nuevo valor y el valor de la referencia.
La tabla siguiente, nos muestra cuáles son las condiciones referenciales, para cada fase en la que se pueda encontrar las sutancias en una reacción química.
- Los valores de actividad, no brindan información sobre la cantidad total de sustancia presente, sino sólo de la cantidad presente en un volumen temperatura dado.
- En las reacciones químicas, tanto las realizadas en los laboratorios, como en los procesos industriales; las soluciones acuosas, o los gases empleados en ellas pueden tener concentraciones o presiones muy disitinta a los valores referenciales, por lo tanto la mayoría de las veces el valor de la actividad será diferente a la unidad.
- Los sólidos y líquidos puros no pueden variar. Ellos serán siempre sólidos y líquidos puros con la misma densidad, en consecuencia estarán siempre en su estado referencial por lo tanto el valor de su actividad será siempre igual a uno.
 |
Ejercicio: Siguiendo esas reglas se puede calcular la actividad de cualquier sustancia si conocemos su fase y su concentración o su presión. Por ejemplo, la actividad de una solución de HCl (ac) de concentración 2,5 M; tendrá una actividad de 2,5 Calcula la actividad para cada uno de los siguientes casos: |
|
Con las definiciones de Cociente de Reacción y de Actividad, podemos ahora calcular, la variación de Energía Libre de Gibbs a condiciones diferentes del estándar:
 |
Problema: Determina la variación de la energía libre de Gibbs a las condiciones propuestas:
N2(g) + 3 H2(g) → 2 NH3(g)
|
|---|---|
| 1.- | |
| Se debe verificar si la reacción está balanceada. | |
| 2.- | |
| Se debe calcular el cociente de reacción Q. Teniendo en cuenta la ecuación química:
Reemplazando los valores se obtiene:
|
|
| 3.- | |
 |
|
| 4.- | |
 |
|
| Conclusiones: | |
|
Si analizamos los valores de la Energía libre de Gibbs a condición estándar y a las condiciones propuestas, podemos observar que la espontaneidad aumenta, el valor a condiciones diferentes del estándar se hace más negativo.
|
Condición de Equilibrio:
Una reacción se encuentra en el equilibrio, cuando en determinado momento durante la reacción, está invierte su sentido. Quiere decir que se van formando productos y en determinado momento, los productos comienzan a producir los reactantes.
Esto solo ocurrirá cuando la variación de la Energía libre de Gibbs sea igual a cero.
Lo que nos permite establecer la siguiente ecuación:
El cociente de reacción, Q, en la condición de equilibrio se conoce como Constante de Equilibrio y se denota con la letraK, luego la ecuación anterior se escribe de la manera siguiente:
Analicemos lo siguiente:
Consideremos que la ecuación química de formación del óxido nítrico, se encuentra en el equilibrio a 25 °C.
N2(g) + O2(g) → 2 NO(g)
podemos plantear la constante de equilibrio:
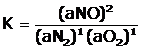
Si el valor de K es mayor de 1, implicará que la reacción ha alcanzado el equilibrio y se ha formado una cantidad considerable de producto. Esto tendrá como consecuencia que el Ln K será un valor positivo.
Si el valor de K es menor de 1, implicará que la reacción alcanzó el equilibrio pero que la cantidad de producto formado es muy pequeña. Esto tendrá como consecuencia que el Ln k será un valor negativo.
Esto se resumen en la tabla siguiente:
