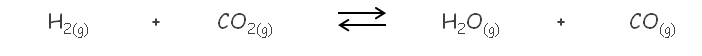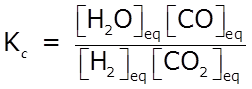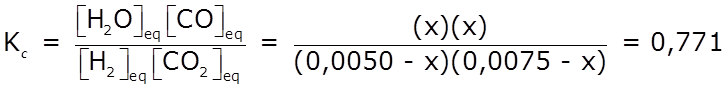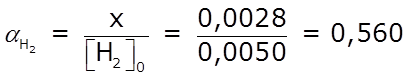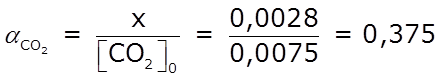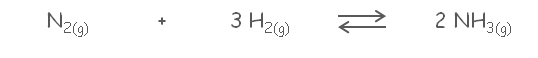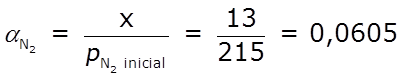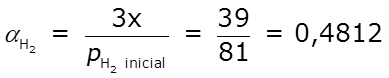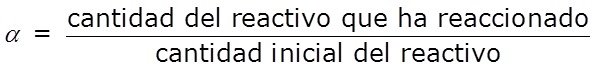3.5. Cálculos una vez alcanzado el equilibrio
Conocida la constante de equilibrio, K, a determinada temperatura, para una reacción específica, se pueden calcular las concentraciones de los componentes de la mezcla en equilibrio, a partir de las concentraciones iniciales, como lo veremos en los siguientes ejercicios.
 |
Ejercicio 1:
Se sabe que a 750 °C, el valor de Kc es 0,771 para la siguiente reacción:
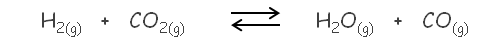 Si colocamos 0,0100 moles de H 2 y 0,0150 moles de CO 2 en un recipiente de 2 L a 750 °C, podemos calcular las concentraciones de cada una de las especies en el equilibrio:
- Determinamos las concentraciones iniciales:
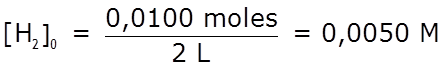 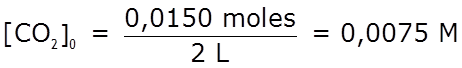
- Hacemos un análisis estequiométrico:
|
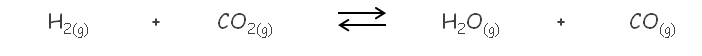 |
| [ ]0 |
0,0050
|
0,0075
|
|
―
|
―
|
| []reacciona |
x
|
x
|
|
―
|
―
|
| [ ]forma |
―
|
―
|
|
x
|
x
|
| [ ]eq |
0,0050 – x
|
0,0075 – x
|
|
x
|
x
|
- Escribimos la expresión de Kc:
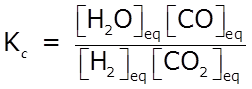
- Reemplazamos las [ ]eq en la expresión de Kc:
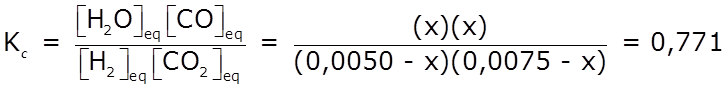
- Determinamos el valor de x:
(0,0000375 – 0,0125 x + x2) 0,771 = x2
⇒ 0,229 x2 + 0,0096375 x – 0,0000289 = 0
⇒ x1 = 0,002811 M ; x2 = – 0,04490 M
Elegimos el valor positivo de x, que a su vez es menor que cualquiera de las concentraciones iniciales. Descartamos el valor negativo de x porque la cantidad que reacciona no puede ser negativa.
- Determinamos las concentraciones en el equilibrio:
[H2]eq = 0,0050 – x = 0,0022 M
[CO2]eq = 0,0075 – x = 0,0047 M
[H2O]eq = [CO]eq = x = 0,002811 M
- Finalmente podemos determinar el grado de reacción, α de cada uno de los reactantes:
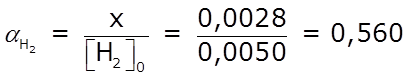 ⇒ la reacción se produjo en un 56,0 % respecto al H2 ⇒ la reacción se produjo en un 56,0 % respecto al H2
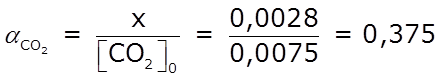
⇒ la reacción se produjo en un 37,5 % respecto al CO2
|
 |
Ejercicio 2
Para la reacción mostrada, se sabe que a 450 °C, el valor de KP = 4,51 x 10-5:
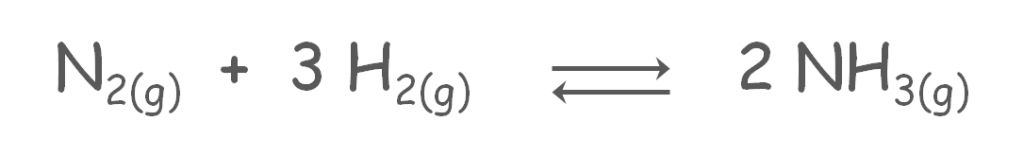 La mezcla inicial contenía 81 atm de H2(g) y 215 atm de N2(g). Una vez alcanzado el equilibrio se determinó que la mezcla consistía en 26 atm de NH3(g), 42 atm de H2(g) y 202 atm de N2(g). La mezcla inicial contenía 81 atm de H2(g) y 215 atm de N2(g). Una vez alcanzado el equilibrio se determinó que la mezcla consistía en 26 atm de NH3(g), 42 atm de H2(g) y 202 atm de N2(g).
|
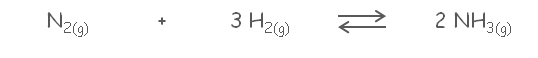 |
| p0 |
215
|
81
|
―
|
| preacciona |
x
|
3 x
|
―
|
| pforma |
―
|
―
|
2 x
|
| peq |
215 –x
|
81 –3 x
|
2 x
|
| de los datos: |
202 atm |
42 atm |
26 |
A partir de la información proporcionada, podemos deducir que x = 13 atm
Determinemos el grado de reacción, α, y el porcentaje que ha reaccionado, 100 α, de cada uno de los reactivos:
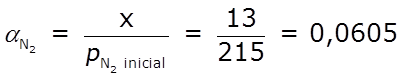 ⇒ ha reaccionado el 6,05 % del N2 ⇒ ha reaccionado el 6,05 % del N2
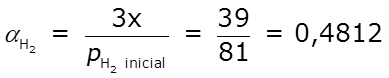
⇒ ha reaccionado el 48,12 % del H2
|
 |
Observaciones
Para determinar las concentraciones en el equilibrio debemos tener en cuenta los siguientes pasos:
- Determinar las concentraciones iniciales.
- Hacer el análisis estequiométrico: expresar las concentraciones de equilibrio de todas las especies en términos de las concentraciones iniciales y una sola variable x que representa el cambio de concentración.
- Escribir la expresión de la constante de equilibrio en términos de las concentraciones de equilibrio.
- Si se conoce el valor de la constante de equilibrio, despejar y obtener el valor de x.
- Calcular las concentraciones de equilibrio.
- El grado de reacción, α, indica en qué proporción se convirtió en producto un determinado reactivo:
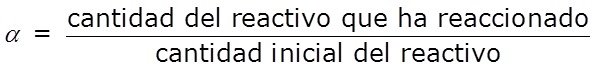
que también puede expresarse en términos de porcentaje de reacción: 100 α
|
 |
Importante
Ten en cuenta que:
- Con frecuencia se llega a expresiones cuadráticas para x:
- Si uno de valores de x es negativo, se descarta
- Si los dos son positivos, se debe elegir el que es menor que las concentraciones iniciales.
- Si el valor de K es del orden de 10–5 o menor que este, se puede aproximar el valor de ( [ ]0 – x ) como [ ]0
|