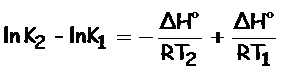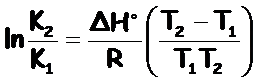3.3. Dependencia de K con la temperatura
A partir de nuestros conocimientos de Termodinámica podemos recordar que:
- ΔG° = – RT lnK
- ΔG° = ΔH° – TΔS°
- Los valores de ΔH° y ΔS° no varían en ciertos rangos de temperatura.
- El valor de la constante de equilibrio depende de la temperatura de reacción.
Podemos plantear las expresiones para dos temperaturas diferentes:
ΔG° = – RT1lnK1 = ΔH° – T1ΔS°
ΔG° = – RT2lnK2 = ΔH° – T2ΔS°
Buscamos una relación que nos indique la dependencia del valor de la constante de equilibrio con la temperatura:
Restamos (2) – (1):
Finalmente, obtenemos la ecuación de Van’t Hoff, expresión que nos indica la dependencia de la constante de equilibrio, K, y la temperatura, T:
| como ΔH tiene unidades de energía ⇒ |  |
Por ejemplo, para el sistema:
Se tiene:
| T (K) | 298 | 348 | 393 | 408 | 423 |
|---|---|---|---|---|---|
| Kp | 0,1124 | 3,8010 | 29,00 | 84,98 | 111,0 |
Podemos observar que conforme se incrementa la temperatura, el valor de K se hace cada vez más grande, es decir, se favorece el sentido directo de la reacción, además, podemos deducir que la reacción es endotérmica.
Lo comprobamos con los valores a 75 °C y 120 °C:
de donde obtenemos que ΔH = 51345,19 J = 51,35 kJ > 0 ⇒ la reacción es endotérmica