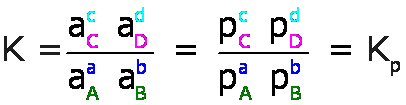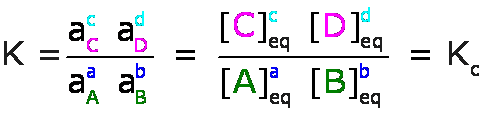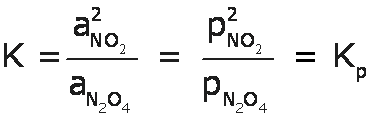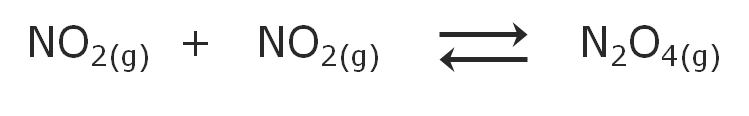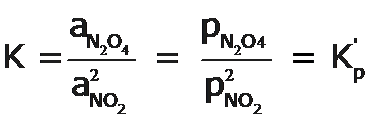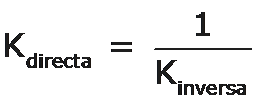3.1.2. Aspecto Termodinámico
Veamos ahora la segunda característica del estado de equilibrio: las cantidades de reactantes y de productos presentes en el equilibrio, permanecen constantes: aspecto termodinámico del equilibrio.
Para una reacción en condiciones no estándar:
ΔG = ΔG° + RT ln Q
Cuando se alcanza el equilibrio termodinámico la energía libre deja de cambiar:
ΔG = 0
Q = K
Entonces: ΔG° = – RT ln K
Donde K es la constante de equilibrio termodinámico.
El análisis de la expresión la podemos resumir en la siguiente tabla:
| K | Ln K | ΔG° | Comentario |
|---|---|---|---|
| > 1 | + | – | Favorece la formación de los productos |
| = 1 | 0 | 0 | Igualmente favorecidos la formación de los reactivos y de los productos |
| < 1 | – | + | Favorece la permanencia de los reactivos |
| Tenemos dos casos extremos: | |
| Si K>>>1: | en el equilibrio, los productos son más abundantes que los reactivos. |
 |
|
| Si K<<<1: | en el equilibrio, los reactivos son más abundantes que los productos. |
 |
|
Para reacciones que involucran sólo gases, las actividades, a, de los gases se expresan en términos de presiones parciales, p, en atmósferas, atm, y la constante de equilibrio se denomina Kp, así por ejemplo, para la ecuación general:
Para las reacciones en soluciones líquidas, las actividades, a, de los solutos se expresan en molaridades, M, y la constante de equilibrio se denomina Kc, así por ejemplo, para la ecuación general:
ésta expresión recibe el nombre de Ley de Acción de Masas.
Para nuestro ejemplo de la descomposicion del N2O4 tendremos:
Y para el proceso inverso, la formación del N2O4 a partir del NO2 tendremos:
 |
Observación La expresión de la constante de equilibrio de la reacción directa es la inversa de la expresión de la constante de equilibrio de la reacción inversa: |
Predicción del sentido de la reacción
|
Para determinar en qué dirección procederá una reacción neta, para alcanzar el equilibrio, se comparan los valores de Q y K, dando lugar a tres posibles situaciones: |
|
| Q>K | para alcanzar el equilibrio, los productos deben transformarse en reactivos, de modo que el sistema procede de derecha a izquierda (los productos se consumen y se forman reactivos). |
| Q=K | el sistema ya está en equilibrio |
| Q<K | para alcanzar el equilibrio, los reactivos deben transformarse en productos, de modo que el sistema procede de izquierda a derecha (los reactivos se consumen y se forman productos). |
Relación entre las diferentes expresiones de K
Si consideramos una reacción general:
![]() A partir de la ecuación general de los gases ideales, PV = nRT, se puede demostrar que la relación entre Kc y Kp es:
A partir de la ecuación general de los gases ideales, PV = nRT, se puede demostrar que la relación entre Kc y Kp es:
|
Kp = Kc (RT)Δn Recordando que pi = xi PT, se deduce la relación: Kp = Kx (PT)Δn |
|
|
Donde: Kp es la expresión de la constante de equilibrio en términos de presiones parciales, en atm. Kc es la expresión de la constante de equilibrio en términos de molaridades, M. Kx es la expresión de la constante de equilibrio en términos de las fracciones molares. |
 |
Importante
|