2.4. Ley de velocidad y orden de reacción
LEY DE VELOCIDAD
Hemos visto que la velocidad de una reacción es proporcional a la concentración de los reactivos. Sin embargo, no todos ellos influyen de la misma manera en la velocidad. La expresión que nos permite calcular la velocidad a la que ocurre reacción y relacionar la velocidad con las concentraciones de los reactivos se llama Ley de Velocidad.
Para una reacción hipotética: A + 2 B → C
Sabemos que la velocidad la podemos expresar así:
Sin embargo, la ley de velocidad nos permite calcular la velocidad, conociendo las concentraciones iniciales de los reactivos. Así, la expresión de la ley de velocidad será:
v = k [A]m[B]n
Donde k (minúscula) es una constante de proporcionalidad denominada constante de velocidad, y m y n son números enteros (mayores o iguales que cero), que NO NECESARIAMENTE son los coeficientes estequiométricos. Es decir, yo no puedo decir que m = 1 y n = 2, ya que estos valores hay que determinarlos experimentalmente. Los números m y n se denominan ÓRDENES PARCIALES DE LA REACCIÓN: “m” con respecto al reactivo A y “n” con respecto a B. La suma de“m+n” nos da el ORDEN TOTAL DE LA REACCIÓN.
Volvamos a nuestra reacción A + 2 B → C
Sabemos que la expresión de la velocidad es: v = k [A]m[B]n
Supongamos ahora, que hemos encontrado experimentalmente los valores de los exponentes: m=1 y n=1. Entonces, podemos decir que la ley de velocidad para la reacción planteada es:
v = k [A][B]
y, por tanto, afirmaremos que:
- La reacción es de primer orden con respecto a la sustancia A.
- La reacción es de primer orden con respecto a la sustancia B.
- La reacción es de segundo orden.
DETERMINACIÓN DEL ORDEN DE LA REACCIÓN: MÉTODO DE LAS VELOCIDADES INICIALES
Sabemos ya plantear la ley de velocidad para una reacción. Nuestro objetivo, entonces, será ahora averiguar los valores de los órdenes parciales de reacción, es decir, los valores de los exponentes “m” y “n”. Como se dijo anteriormente, estos valores se determinan experimentalmente.
El método más simple para determinar los órdenes parciales de reacción consiste en el método de las velocidades iniciales.
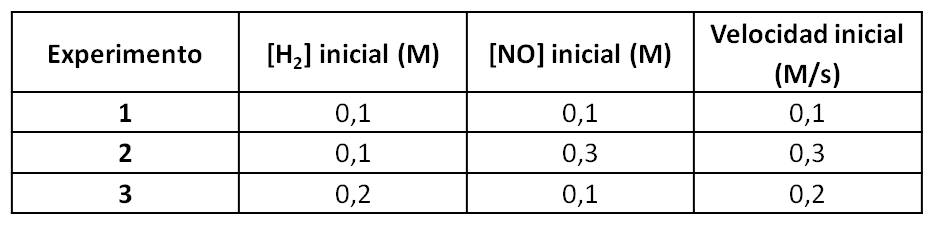
Analicemos la siguiente reacción, utilizada para eliminar el óxido nitroso (NO), un contaminante gaseoso, usando hidrógeno (H2). Observa que los productos son inocuos.
2 H2(g) + 2 NO(g) → N2(g) + 2 H2O(g)
La ley de velocidad de esta reacción está dada por: v = k [H2]m[NO]n
Recuerda que m y n no son necesariamente los coeficientes estequiométricos: no se puede asumir que m=2 y n=2, hay que calcularlo.
Para determinar los órdenes parciales, se mide la velocidad inicial de la reacción (variación de concentración en función al tiempo) al variar las concentraciones iniciales de los reactivos, a cierta temperatura. Así, se ha encontrado que:
Estos datos los podemos reemplazar en la ecuación de la ley de velocidad. Así, usando los datos de cada experimento, tendríamos:
Experimento 1: 0,1 M/s = k [0,1 M]m[0,1 M]n (ecuación 1)
Experimento 2: 0,3 M/s = k [0,1 M]m[0,3 M]n (ecuación 2)
Experimento 3: 0,2 M/s = k [0,2 M]m[0,1 M]n (ecuación 3)
Dividamos ahora la ecuación 1 entre la ecuación 2:
Eliminando unidades del numerador y denominador, observamos también que aquellas expresiones con exponente “m” también se eliminan, por tanto, nos queda:
o, lo que es igual: 0,33 = (0,33)n. Por tanto, n = 1
Dividamos ahora la ecuación 1 entre la ecuación 3:
Al eliminar unidades en común y aquellas expresiones con exponente “n” (en este caso), obtenemos:
0,5 = (0,5)m. Por tanto, m =1
De esta forma, hemos determinado los órdenes parciales de la reacción: la reacción es de primer orden (m=1) con respecto al hidrógeno, y de primer orden (n=1) con respecto al óxido nitroso. En consecuencia, el orden total de la reacción es 2, o, dicho en otras palabras, la reacción es de segundo orden. Por tanto, la ley de velocidad es:
v = k [H2][NO]
La ley nos dice entonces, que la velocidad depende directamente de las concentraciones de ambos reactivos. Existen casos en los que la velocidad no depende de la concentración de alguno de ellos (reacciones de orden cero), es decir, la velocidad es independiente de la cantidad de reactivo que se tenga.
Conociendo los valores de los órdenes parciales, podemos calcular el valor de la constante de velocidad, reemplazando los datos dados en cualquier ecuación. Usemos la ecuación 1:
Resolviendo, obtenemos que la constante es: k = 10 M-1s-1
Ten en cuenta las unidades de la constante: dependen del orden de la reacción. Asimismo, recuerda que “k” es una constante: debe tener el mismo valor en todos los casos.