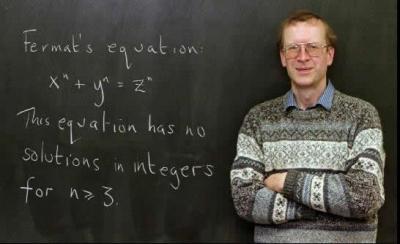
Pierre de Fermat, jurista francés del siglo XVII es conocido como el padre de la teoría de números. Sus contribuciones abarcan los números perfectos, los números amigos, los números de Fermat (su gran batacazo), el pequeño teorema de Fermat (generalizado más tarde por Euler)…
Gran parte de culpa de este interés de Fermat por la teoría de números la tuvo un ejemplar de la Arithmetica de Diofanto de Alejandría que llegó a sus manos. A través de ese libro Fermat comenzó a estudiar propiedades de los números, y en este libro nos dejó su afirmación más enigmática desde su época hasta nuestros días. Por ser la afirmación de Fermat que más se ha tardado en demostrar se denomina último teorema de Fermat:
Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exigitas non caperet.

La traducción dice así:
Es imposible dividir un cubo en suma de dos cubos, o un bicuadrado en suma de dos bicuadrados, o en general, cualquier potencia superior a dos en dos potencias del mismo grado; he descubierto una demostración maravillosa de esta afirmación. Pero este margen es demasiado angosto para contenerla.
Fermat se refiere a esto:
Para el siglo XVII Fermat tenía una demostración de este resultado, y teniendo en cuenta los genios de las Matemáticas que aparecieron después (Euler, Cauchy, Gauss, Lagrange…) no debería ser demasiado complicado encontrarla. Pero nada menos que 350 años tuvieron que pasar hasta que Andrew Wiles consiguiera demostrar este resultado deduciéndolo como corolario de otro resultado mucho más complicado (conjetura de Shimura-Taniyama-Weil) y que, en principio, no tenía nada que ver con el resultado propuesto por Fermat. Teniendo en cuenta que Fermat no disponía de todas las herramientas que usó Wiles, que la demostración ocupa más de 100 páginas y que en 350 años ningún matemático fue capaz ni tan siquiera de acercarse a una demostración del caso general del problema (sólo se consiguió demostrar casos particulares del mismo) lo más lógico es pensar que aunque Fermat pensaba que poseía esa demostración maravillosa en realidad estaba equivocado, ya que cuesta entender que en tanto tiempo y con tantos matemáticos brillantes dedicados en mayor o menor medida al tema ninguno llegara a la demostración de este hecho.
Y claro, 350 años dan para mucho. Muchas anécdotas e historias en torno a esta afirmación: miles de demostraciones falsas propuestas para su estudio, piques entre matemáticos para ver quién llegaba antes a la prueba definitiva, desesperación de genios como Euler o la participación de una de las (por desgracia) pocas mujeres con contribuciones importantes en Matemáticas a lo largo de la historia. Su nombre era Sophie Germain, y para evitar que los matemáticos varones de la época la ignoraran tuvo que adoptar un seudónimo: monsieur Leblanc.
Pero bueno, al fin en 1993 Andrew Wiles presenta su demostración del teorema y se acaba la historia, final feliz y todos contentos…pues no. Parece que este resultado perseguía de una u otra forma a quien intentaba abordarlo. Wiles presenta su demostración en edad para recibir la medalla Fields (sólo se entrega a matemáticos hasta 40 años). Pero en el correspondiente período de revisión se encuentra un error que Wiles, junto a Richard Taylor, tarda en resolver cerca de 2 años…pasando en ese tiempo la edad máxima para recibir el premio. Aún encontrando la demostración la maldición del último teorema de Fermat continuaba de cierta manera, aunque más tarde se reconoció la labor de Wiles con el premio Wolfskehl, consistente en una cantidad en metálico dejada por el matemático del mismo nombre en su testamento y la evidente admiración de toda la comunidad matemática.
Por cierto, fue tal la trascendencia de la demostración que el señor Wiles apareció en portada del New York Times por este hecho. Encontrar la demostración de un resultado que ha permanecido abierto durante 350 años no se consigue todos los días.
Fuentes de la nota:
http://www.fafamonge.com/2008/02/ultimo-teorema-de-fermat.html
http://gaussianos.com/el-ultimo-teorema-de-fermat/
Amigo lamentablemente despues de la muerte de euler hasta nuestros días no existe otro matematico que cultive la razón pura de llamarla a la matematica una ciencia exacta; hasta la misma impaciencia de Gauss nos a transportado aun mundo de la ciencia que hoy se conoce mundo de posibilidades (principio de incertidumbre fisica cuantica), por esa razón la tediosa forma de explicar un sin numero de conjeturas matematicas para su demostración hoy resulte sumamente perezoso; en fin te recomiendo leer matematicafilosofica.blogspot hago un pequeño comentario sobre el ultimo teorema de fermat que para mi entender la solució de Andrew Willes es simplemente aburrida.
Euler manifest¨® que cre¨ªa que Fermat sabia como demostrar su conjetura y adem¨¢s Euler demostr¨® que X^n+Y^n©¤Z^n¡Ù0 cuando n=3 y con X,Y,Z racionales enteros positivos no nulos; que a la vez evidencia en general que esta diferencia es tanto m¨¢s grande que 0 cuanto m¨¢s grande es la secuencia progresiva del grado de potencia n-en¨¦simo mayor que 3.
saludos… me gustaria saber si tiene algun tipo de informacion q hable de una supuesta afirmacion q tiene fermat que dice mas o memos asi "26 es el unico nuemero q se encuentra entre un cuadrado perfecto y un cubo perfecto"
25 – 26 – 27
5^2…..3^3
me gusta la cony <3 xd
a el teorema muy bueno
valla puedo llegar a la casa de mi vecino dandole la vuelta al mundo o simplemente saltando la verja que nos divide, en serio tengo la solucion verdadera ha este problema la que fermat tenia y creamne es mas sencilla exacta maravillosa y verdadera que la de wiles y no la han descubierto por lo que fermat dejo escrito, que no cabe aqui por ser este margen muy estrecho,demasiado diria yo era un genio fermat como hago para que la vieran ustedes creanme hasta aqui llego este dilema que todavia no se puede decir caso cerrado hasta que vean lo que tengo que demostrarles
?what happened to MY solution?
I published 1992 in internet and it was accepted by many people.
My name is
Ing. Jorge Humana Zunoino
jhumanaz@hotmail.com