El enfoque de la planificación estratégica minera es conducir la explotación (mina – mercado) a su óptima captura de valor y asegurar la sostenibilidad de la operación y que permita a su gestión el desarrollo de sus planes de valor compartido. Por tanto la planificación de la producción minera es un tema muy importante del proceso de diseño de la mina y ello involucra entre otros puntos claves determinar la estrategia de ley de corte que maximice el valor del proyecto.

Un caso descriptivo, una empresa minera anuncio a su directorio, como resultado final de una agresiva campaña de exploraciones durante un año, la existencia potencial adicional de 1 Millón de onzas de cobre, lo cual fue recibida y difundida de gran manera en el sector. La siguiente pregunta aquí es; cuanto de los recursos anunciados implican aporte de valor real a la corporación, o cuanto de sus recursos anunciados serán económicamente explotables, a que costo, en cuanto tiempo será posible generar un flujo de efectivo que ponga en valor al proyecto y pueda sosteniblemente asegurar la generación de valor entre sus grupos de interés.

Si bien es cierto consolidar los recursos es una etapa importante en la maduración y continuidad del negocio minero, no es la etapa final, pues continua la puesta en valor desde una perspectiva global que involucra aspectos técnicos, económicos, sociales y ambientales. Por ello es importante definir un modelo robusto de las reservas y el valor económico que la sustenta en un marco social y ambiental responsable. Como es ampliamente conocido, la estimación de las reservas se determina en función de un robusto modelo geotécnico, geometalúrgico, hidrogeológico y económico (mercado, precios, penalidades, cargos de fundición, refinación, regalías, etc.) principalmente.

Una manera de maximizar el valor (Valor Actual Neto, VAN) de un yacimiento minero es determinar una óptima estrategia de ley de corte, esta técnica es ya desarrollada pero poco aplicada en la industria minera. Se ha observado que a diferencia de aplicar una constante ley de corte de equilibrio (breakeven cutoff grade), por una óptima y dinámica ley de corte, que cambia debido al efecto decreciente del VAN durante la vida de la mina, y no solo por respetar el precio del metal y los costos de las etapas de mina, molienda y refinación, sino también por tomar en cuenta las restricciones de capacidad de estas etapas y la distribución del tonelaje-ley del depósito (Dagdelen 1992, Lane 1988, Dagdelen & Mohammad 1997). En otras palabras, la técnica que determina la estrategia de ley de corte, considera el costo de oportunidad de no recibir antes el flujo de caja futuro durante la vida de la mina, debido a las limitaciones de capacidad de cualquiera de las etapas de minería, molienda o refinación (Lane 1964 & Mohammad 1997).

Lane (Lane, 1964) propuso un algoritmo para determinar la ley de corte que maximiza el VAN de un proyecto sujeto a restricciones de capacidad de mina, tratamiento y refinación. La estrategia de ley de corte que resulta en un mayor VAN para un proyecto dado inicia con altas leyes de corte durante los años iniciales de explotación. A medida que la explotación avanza, las leyes de corte gradualmente disminuyen hasta alcanzar la ley de corte de equilibrio según la distribución de la ley del depósito. La aplicación de este algoritmo en la determinación de la óptima estrategia resulta en la mejora significativa en el valor del proyecto.

Este artículo describe los beneficios sustanciales de la aplicación de una estrategia de ley de corte a lo largo de la vida de la mina basado en el algoritmo de Lane (Lane, 1964) adicionando un factor de optimización basado en el algoritmo de gradiente reducido generalizado (GRG) que maximiza el VAN del proyecto (Nieto & Bascetin, 2006), para ello, se mostrara un ejemplo comparativo.

El proceso para determinar la ley de corte anual, incorporar el factor de optimización (σ) que se incluye en la ecuación de la ley de corte última, que considera el costo de minado (m), para maximizar aún más el VAN total del proyecto minero. Además el proceso incluye y resuelve el factor de optimización (σ), que es un problema no lineal (NLP), basado en el algoritmo de gradiente reducido generalizado (GRG), al maximizar el VAN del proyecto.

El ejercicio desarrollado incluye tres escenarios:

1.- Se desarrolló un plan considerando una ley de corte de planta que es constante a lo largo de la vida de la mina.

2.- Plan considerando una ley de corte de planta más el costo de minado y un factor de costo oportunidad.

3.- Plan considerando una ley de corte igual al escenario 2 más el factor de optimización (σ) para encontrar el máximo valor.

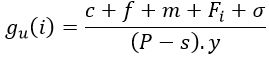
Descripción de la ecuación para determinar la ley de corte última más el costo de oportunidad y el factor de optimización.

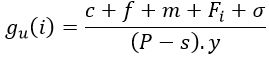
Donde:

c: Costo de Procesamiento      f: Costo Fijo                              m: Costo de Minado

Fi: Costo de Oportunidad        σ: Factor de Optimización      P: Precio del Metal

s: Costo de Venta                      y: Recuperación metalúrgica

El costo de oportunidad es determinado como:

El costo fijo por tonelada es determinado como:

Donde  fa: Costos fijos anuales  C: Capacidad de la molienda

Figura 1. Esquema de disposición del material hacia la mina, planta o stockpile de acuerdo a la variación de la ley de corte en el tiempo, objetivo final maximizar el valor presente neto.

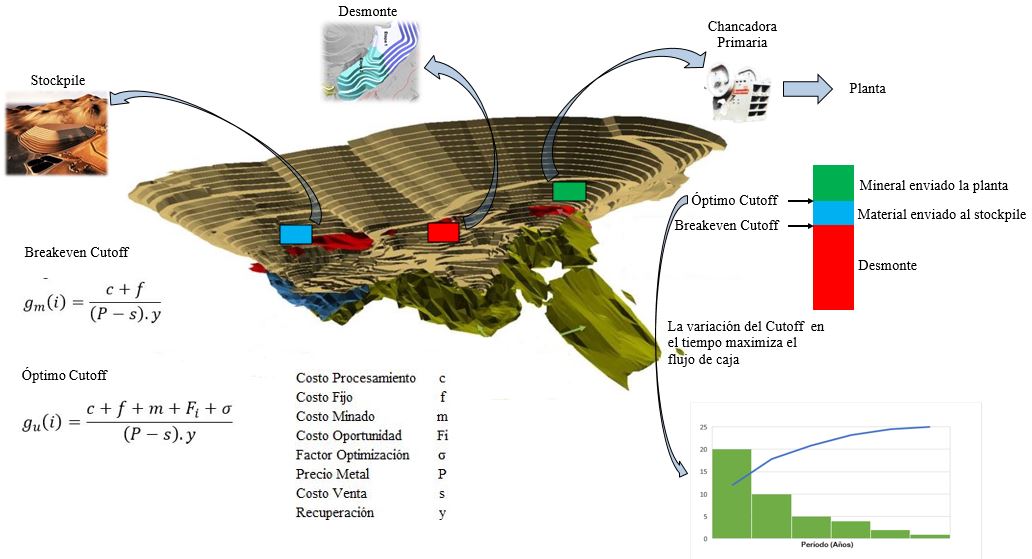
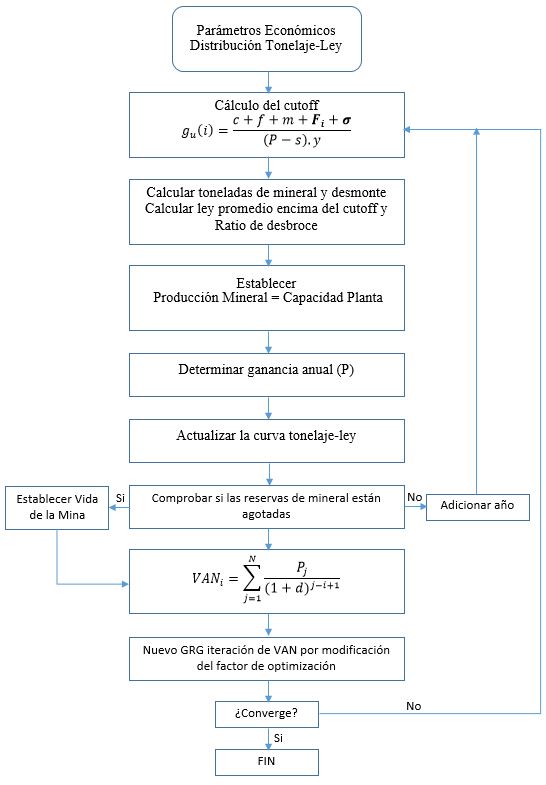
Figura 2. Algoritmo para determinar la estrategia de ley de corte (Nieto & Bascetin 2006).

Fuente: Cutoff grade and NPV optimization, Dr. Antonio Nieto

Resultados de los escenarios.

Figura 3. Escenario 1

Figura 4. Escenario 2

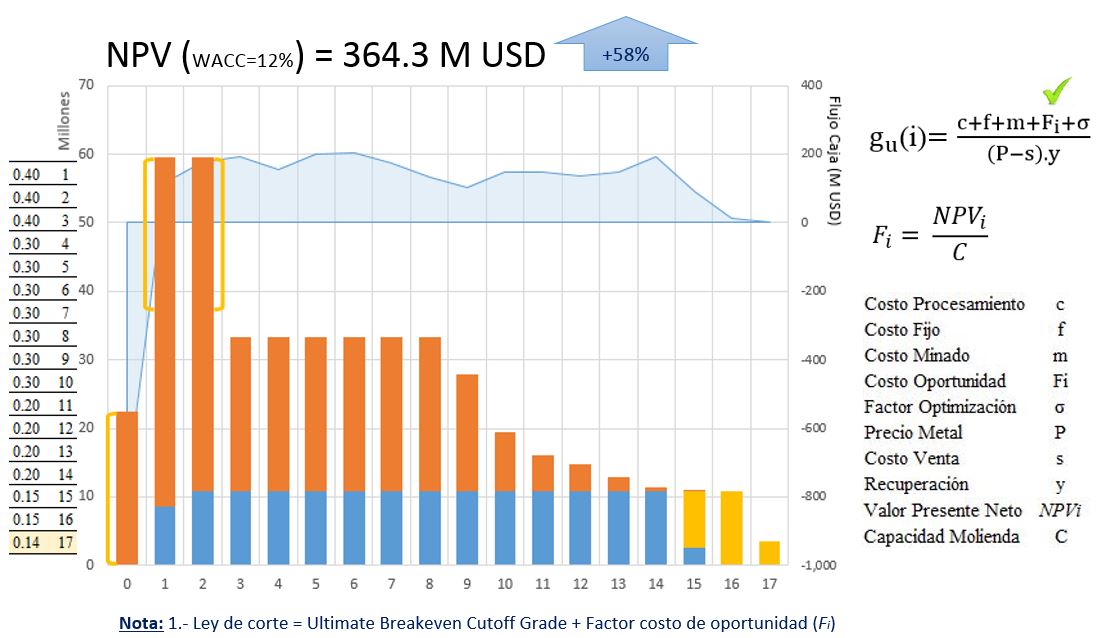
Figura 5. Escenario 3

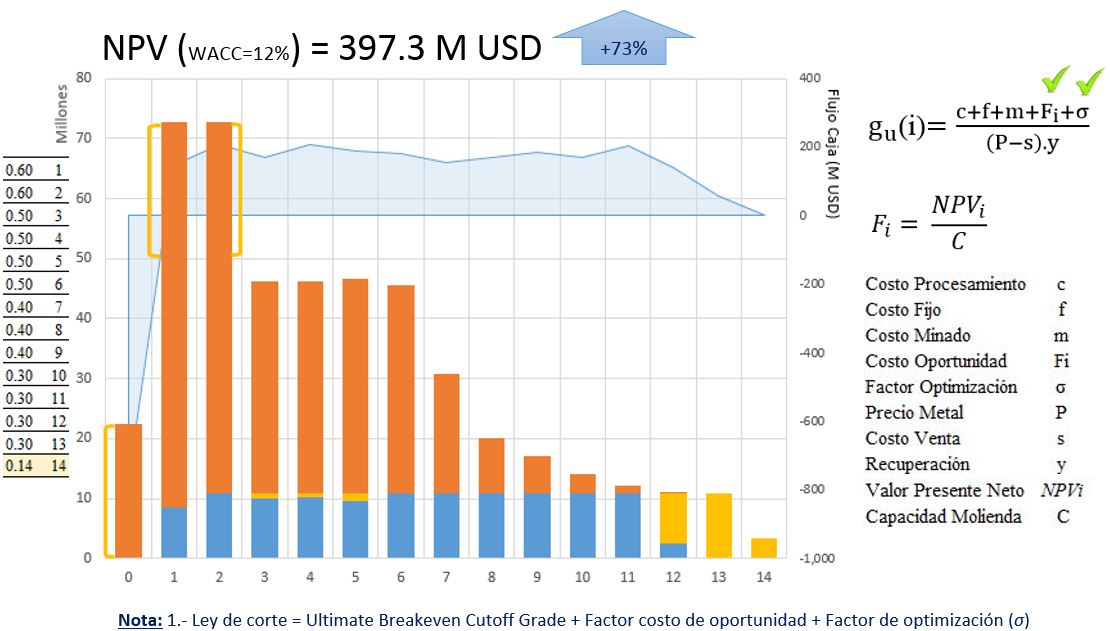
Observaciones

Al aplicar la metodología (Nieto & Bascetin 2006) para definir una estrategia de ley de corte, requiere de un estudio para la implementación y diseño de un stockpile de mineral de baja ley, que permitirá alcanzar y priorizar el mineral de alta ley.

Por otro lado, la ley de corte óptima es de naturaleza dinámica en dos aspectos: 1.Cambia con el tiempo (periodos mineros) y 2. El espacio (zonas mineras). El trabajo de Lane da cuenta de la naturaleza dinámica de la ley de corte a lo largo del tiempo, lo que resulta en diferentes leyes de corte en diferentes períodos de la explotación, pero este algoritmo (Figura 2) al usar la distribución de la ley de la totalidad de la reserva minera, no aborda la naturaleza dinámica de la ley de corte con respecto al espacio o lugares en los que se planea la explotación minera. Esta es una seria limitación, ya que en algunos depósitos, hay una marcada diferencia entre zonas (alteración, litología, estructural, etc.) reflejado en diferentes distribuciones de ley de mineral y, al ignorar dicha variación, se obtendrán políticas de ley de corte poco prácticas. En un depósito donde la ley del mineral es bajo en la parte superior y alto en la parte inferior, el uso de las leyes de corte más altos en la etapa temprana no sería apropiado y puede que no sea práctico debido a la ausencia de mineral de alta ley en la parte superior

¿Cómo podemos abordar la naturaleza dinámica de la ley de corte con respecto al espacio? En lugar de evaluar la total distribución de tonelaje-ley, debemos considerar las distribuciones de múltiples leyes, una por zona de explotación. Para minas a tajo abierto, cada fase puede tratarse como una zona minera con su propia distribución de ley y para minas subterráneas, cada tajeo (stope) o un grupo de tajeos puede tratarse como una zona de explotación minera, nuevamente con su propia distribución de ley.

Conclusiones

La ley de corte (Cut-off grade) es uno de los parámetros más importantes en la planificación estratégica de la mina. La elección de las mejores leyes de corte que maximizan el valor presente neto (VAN) ha sido un tema de investigación importante desde la década de 1960. El trabajo de Lane ha sido considerado como un hito en la optimización de la ley de corte. Su modelo apunta a maximizar el VAN, sujeto a las limitaciones de capacidad de las etapas de extracción, concentración y refinación, así como al equilibrio de capacidad de las tres etapas (Lane 1965).

Como se observa en los resultados finales hay un significativo incremento del valor del negocio en los escenarios 2 y 3 respecto a la tradicional metodología de optimización, escenario 1. Por otro lado es necesario para llegar al mineral de alta ley, en este ejercicio, la planificación de una campaña de desbroce en los años 0, 1 y 2 (Figuras 4 y 5). Estos planes están sujetos a una evaluación operativa de disponibilidad de espacios físicos para albergar: el stockpile de baja ley, así como para el desbroce inicial de los primeros años.

Si la preocupación es que los límites de mineral en algunas leyes de corte no pueden definirse adecuadamente con los datos actuales, esto no debe ser un problema. El propósito del estudio es identificar estrategias, no producir diseños detallados para la implementación en el futuro inmediato. Como en todas las situaciones, si el problema se puede describir, en teoría se puede modelar y evaluar.